【JS体操】第2問「画像の横長具合を比較しよう」〜正攻法＆ハック部門の解説〜

こんにちは！
カヤック面白プロデュース事業部のおばらです。
普段は受託案件のデザイン・フロントエンド開発などを担当しています。

さて、『JS体操』第2問 いかがでしたか？

• 今回初めての方々
• 第1問に引き続きの方々
• 複数のアプローチで何通りも回答してくださった方々
• 普段業務で JavaScript をバリバリ書いているであろう方々
• JavaScript を学んでいる学生の方々

などたくさんの方々が挑戦してくださいました。
とても嬉しいです。ありがとうございます！

『JS体操』とは？

『JS体操』とはカヤックが主催する JavaScript のコードゴルフ大会です。
もともとは社内の勉強会として始めた施策です。
その詳細は以下のブログ記事を御覧ください！

techblog.kayac.com

第2問の詳細はこちら

https://hubspot.kayac.com/js-taiso-002

もしまだ挑戦できていなかった！という方はぜひ。 今回は（第1問以上に）いろんなアプローチで解くことができるようになっていますよ！

hubspot.kayac.com

まずは最短文字数の発表

正攻法 66文字

正攻法はきちんと画像の横長具合を比較する正統派部門です。 見事、66文字を達成された方は以下の2名！おめでとうございます！

🥇ぺち さん
🥇halwhite さん
（※ Unicode コードポイント順）

export default(a,b,f=e=>e.naturalWidth/e.naturalHeight)=>f(a)-f(b)

ハック部門 33文字

33文字を達成された方は、、、

🥇undefined

いませんでした！

export default()=>9e9<<length+++9

33文字を達成された方はいませんでしたが、面白いアプローチの回答をいくつかご紹介します！

let r=1284*7**7;export default()=>r<<=2 // 39文字（tkihira さん）

let r=28954<<16;export default()=>r<<=1 // 39文字（tkihira さん）

let i=0x711a0000;export default _=>i<<=1 // 40文字（karuru6225 さん）

export default()=>(302680704>>2*length++&3)-1 // 45文字

let c=14;export default()=>c&&(1906>>--c&1)-.5 // 46文字

let c=10096;export default()=>c&&((c>>=1)&1)-.5 // 47文字

let c=22670;export default()=>(c>>=1)&&.5-(c&1) // 47文字

let i=0;export default x=>"000222022200201"[i++]-1 // 50文字（ほーく さん）

let x=1;export default()=>((x<<=1)&10096)-(x&22670) // 51文字（弊社 mashiike）

let i=0;export default()=>[3,4,5,7,8,9,12].includes(i++)?1:i>14?0:-1 // 68文字（弊社 mashiike）

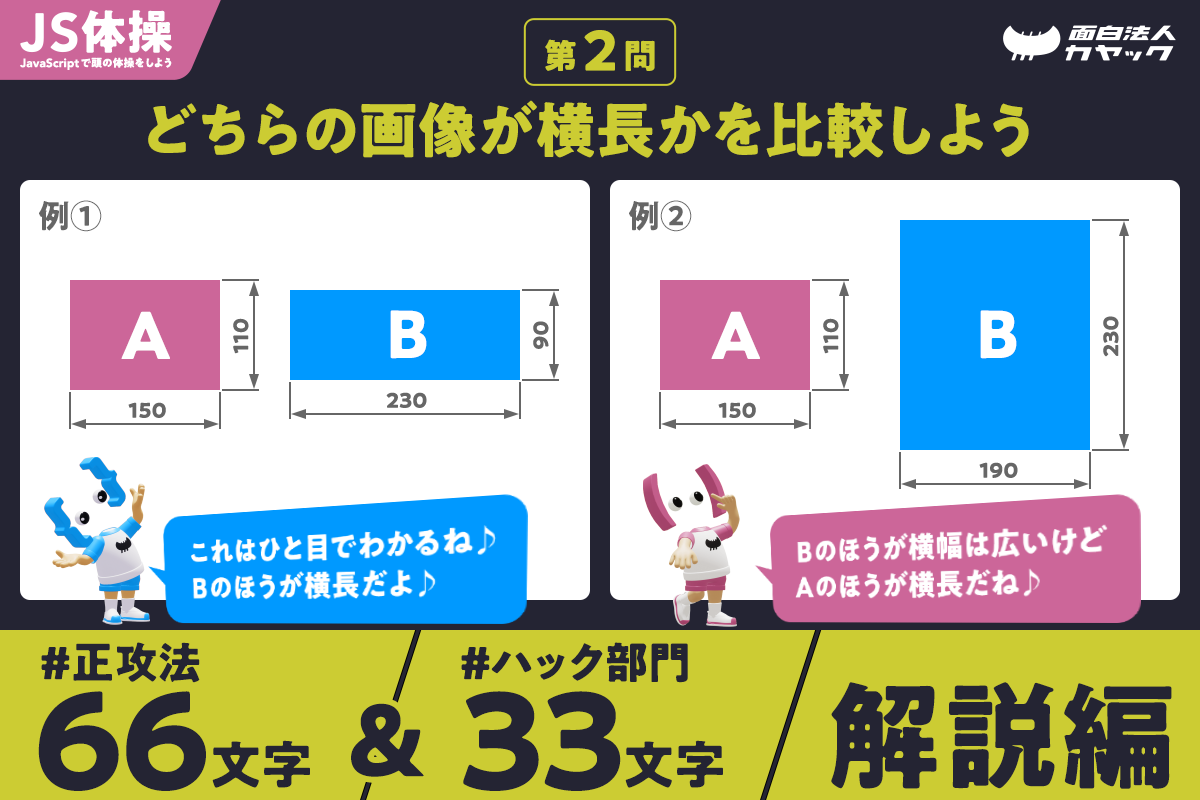
解説の前に問題のおさらい

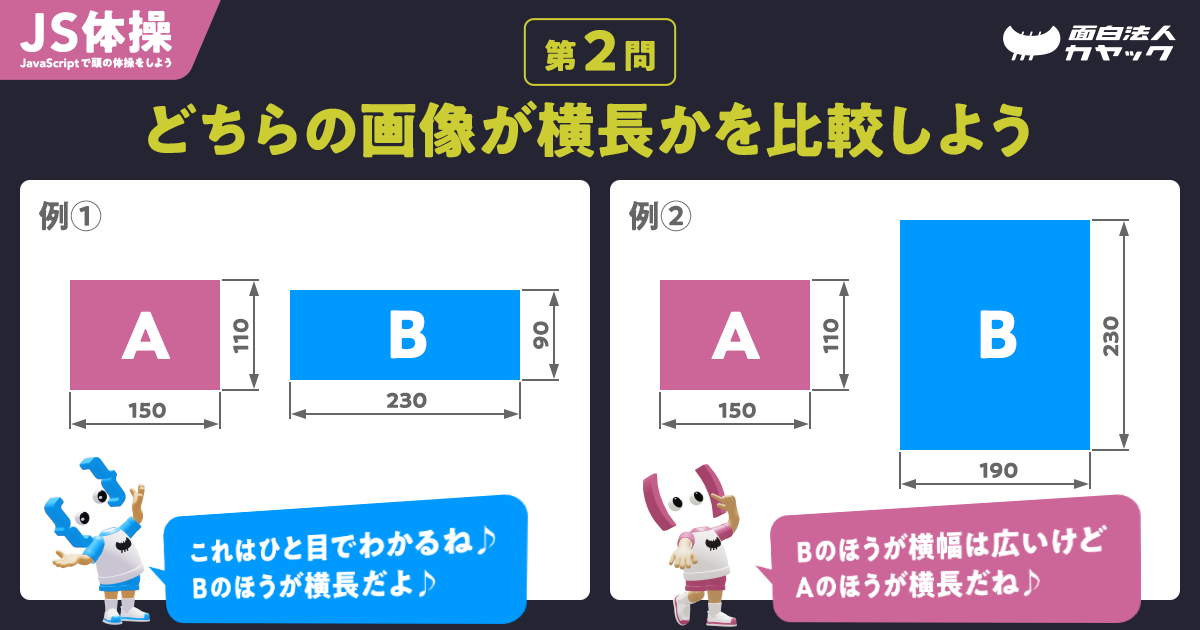
『JS体操』第2問 は2つの画像の「横長具合」を比較する問題。 Canvas2D やWebGL などで特定の領域に任意サイズの画像をピッタリ収めたい時などに必要なロジックです。

また、今回は（第1問以上に）いろんなアプローチで解くことができました。

本記事ではそのうち

• 「正攻法」66文字
• 「ハック部門」33文字

を解説します。

• 禁断の「チート部門」3種

に関してはまた別の記事でお届けします。
しばらくお待ちください！

正攻法66文字の解説

export default(a,b,f=e=>e.naturalWidth/e.naturalHeight)=>f(a)-f(b)

横長具合とは

問題文では「横長具合」というあいまいな表現をあえて使っていましたが「横長具合」とは一体何でしょう？

横方向に長いこと？横の幅に比べて縦の高さが小さいこと？縦長の逆？説明が難しいですね。でも皆さんご存知、「縦横比」という言葉で説明してしまえば一発です！

「縦横比（じゅうおうひ）」もしくは「アスペクト比（Aspect Ratio）」という言葉・概念は広く知られて（しまって）いるので、「横長具合」を比較するには「縦横比」を比較すれば良いという結論・事実を知っている方は多いでしょう。

ところで「縦横比」というと「横の幅を縦の幅で割った数値」、つまり「横の幅と縦の幅の比」、と私は認識していたのですが、はてブに頂いたコメントをきっかけに調べてみると「縦横比」ではなくあえて「横縦比（おうじゅうひ？よこたてひ？）」と表記する場合もあるようですね。 たしかに「横」を「縦」で割っているので「縦横比」ではなく「横縦比」と呼んだほうががしっくりくる気がしなくもない、、、あ、「縦」分の「横」（たてぶんのよこ）と考えれば「縦横比」のがしっくり来る？謎です。

本記事ではより一般的だと思われる「縦横比（じゅうおうひ）」という言葉で説明しようと思います。
（2024/06/19 追記）

さて、「縦横比」or「横縦比」の謎は気になるところではありますが、「横の幅と縦の幅の比」という概念は皆さん知っていると思います。ここではあえて比をとる意味を深堀りしてみましょう。 まずは問題のリファレンス実装（compare.js の初期状態のコード）を見てみます。

// このファイル（compare.js）をなるべく少ない文字数で書き直してください♪
// main.js でエラーが出なければ（main.js のテストに合格すれば）OK です♪
// このファイル（compare.js）のみ編集可能です♪

/**
 * 2つの画像のどちらがより横長かを比較する
 *
 * img1 よりも img2 のほうが横長 => 負
 * img1 のほうが img2 よりも横長 => 正
 * img1 も img2 も同じくらい横長 => 0
 *
 * @param  {HTMLImageElement} img1
 * @param  {HTMLImageElement} img2
 * @return {number}
 */
export default function compare(img1, img2) {
  //
  // 各画像の幅と高さを変数に格納しておく
  //
  const w1 = img1.naturalWidth;
  const h1 = img1.naturalHeight;

  const w2 = img2.naturalWidth;
  const h2 = img2.naturalHeight;

  //
  // 方針：
  // ① まずは幅をチェックする
  // ② つぎに高さをチェックする
  //

  //
  // w1 < w2、
  // つまり、
  // img1 よりも img2 のほうが幅が広い時
  // img1 よりも img2 のほうが横長？？？
  //
  if (w1 < w2) {
    // h1 < h2、
    // つまり img1 よりも img2 のほうが高さが（も）高いなら
    // 結果が逆転する可能性がある
    if (h1 < h2) {
      const rw = w2 / w1; // 幅がどれだけ差があるか
      const rh = h2 / h1; // 高さがどれだけ差があるか

      // 高さの影響が大きい場合
      if (rw < rh) {
        return 1;

      // 幅の影響が大きい場合
      } else if (rw > rh) {
        return -1;

      // どちらも同じの場合
      // w1 < w2 の横長具合への影響は影響は相殺される
      } else {
        return 0;
      }

    // h1 > h2 なら
    // img1 はより縦長に、img2 はより横長にしかなり得ないので
    // img1 よりも img2 のほうが横長であることが確定する
    } else if (h1 > h2) {
      return -1;

    // 高さが同じなら
    // img1 よりも img2 のほうが横長であることが確定する
    } else {
      return -1;
    }

  //
  // w1 > w2 つまり、
  // img1 のほうが img2 よりも幅が広い時
  // img1 のほうが img2 よりも横長？？？
  //
  } else if (w1 > w2) {
    // h1 < h2 なら
    // img1 はより横長に、img2 はより縦長にしかなり得ないので
    // img1 のほうが img2 よりも横長であることが確定する
    if (h1 < h2) {
      return 1;

    // h1 > h2 なら
    // 結果が逆転する可能性がある
    } else if (h1 > h2) {
      const rw = w1 / w2; // 幅がどれだけ差があるか
      const rh = h1 / h2; // 高さがどれだけ差があるか

      // 高さの影響が大きい場合
      if (rw < rh) {
        return -1;

      // 幅の影響が大きい場合
      } else if (rw > rh) {
        return 1;

      // どちらも同じの場合
      // w1 > w2 の横長具合への影響は影響は相殺される
      } else {
        return 0;
      }

    // 高さが同じなら
    // img1 のほうが img2 よりも横長であることが確定する
    } else {
      return 1;
    }

  //
  // 幅が同じ場合は、高さだけで結果が決まる
  //
  } else {
    // img1 のほうが img2 よりも横長
    if (h1 < h2) {
      return 1;

    // img1 よりも img2 のほうが横長
    } else if (h1 > h2) {
      return -1;

    // img1 も img2 も同じくらい横長
    } else {
      return 0;
    }
  }
}

とーっても冗長ですね。 あまりに冗長すぎて、まずはこれを一切見ずに全消しするところからスタートした方も多いのではないでしょうか。

問題を作った私も「縦横比」という概念をあえて使わずに書くのが大変でした。今回はそれが一番大変だったと言っても過言ではありません。はたしてこの冗長なロジックは正しいのでしょうか？ テストに通っているので多分正しいのでしょう。でももっとシンプルにスマートに書けますね！

正規化・無次元量化

リファレンス実装の大きな問題点は、単位が「px」の世界（次元）で比較をしようとしている点です。こういった場合は

• 値を正規化する（無次元量化する）

と楽ですね！

つまり、px を px で割り、

で「px」を約分（という言い方が正しいかは置いておいて）し、「px」の世界（次元）から解放してあげればよいわけです。

もちろん分子と分母が逆でも（正規化・無次元量化するという目的であれば）何の問題もありません。

「px」という単位から開放されるだけでなく、「横幅」と「縦幅」という2つパラメータを「縦横比」という1つのパラメータとして扱えることも大きなメリットですね。

このように、値を正規化・無次元量化するという考え方が便利な瞬間（強制される瞬間も）は 普段の（JavaScript を使う）業務でも良くあります。例えば WebGL でシェーダ、特に頂点シェーダをゴリゴリ書く時など！ 記事の最後に WebGL を使った応用例も載せましたのでぜひご覧ください。

縦横比の比較

正規化・無次元量化の話が長くなりましたが、要は2つの画像の横幅を縦幅で割った「縦横比」同士を比較すれば良いです。 まずは素直に JavaScript で書いてみましょう。

export default function compare(img1, img2) {
  const aspectRatio1 = img1.naturalWidth / img1.naturalHeight;
  const aspectRatio2 = img2.naturalWidth / img2.naturalHeight;

  return aspectRatio1 - aspectRatio2;
}

どんどん短くしていきましょう！変数を1文字にします。

export default function compare(a, b) {
  const n = a.naturalWidth / a.naturalHeight;
  const m = b.naturalWidth / b.naturalHeight;

  return n - m;
}

一時変数 n と m に格納するのもやめます。

export default function compare(a, b) {
  return a.naturalWidth / a.naturalHeight - b.naturalWidth / b.naturalHeight;
}

アロー関数にします。

export default (a, b) => {
  return a.naturalWidth / a.naturalHeight - b.naturalWidth / b.naturalHeight;
};

return を省略します。

export default (a, b) => a.naturalWidth / a.naturalHeight - b.naturalWidth / b.naturalHeight;

ホワイトスペースやセミコロンなど、省略できるものを省略します。

export default(a,b)=>a.naturalWidth/a.naturalHeight-b.naturalWidth/b.naturalHeight

だいぶ短くなりました！

共通部分をまとめる

• a.naturalWidth/a.naturalHeight
• b.naturalWidth/b.naturalHeight

がほぼ同じなので関数にまとめましょう。

const f=e=>e.naturalWidth/e.naturalHeight;
export default(a,b)=>f(a)-f(b)

const vs. let vs. var

const が長いので省略したいですね。 でも compare.js はモジュールとして読み込まれているので「厳格モード（Strict Mode）」扱いです。 よって const や let、 var を省略し暗黙的にグローバル変数 f を宣言することはできません。残念。

そこで、少しでも文字数が短い let もしくは var にしちゃいましょう。 懐かしの var は実際の業務では今後ほぼ使うことはないですが、コードゴルフではたまに var 特有の挙動を求めて使うこともあるかもしれませんね！

f は再代入しないので本来（実際の業務）であれば let ではなく const にしたい派閥の方が多いと思いますが、ここは断腸の思いで let にします。

let f=e=>e.naturalWidth/e.naturalHeight;
export default(a,b)=>f(a)-f(b)

2文字短くなりました。

変数宣言を短くする（デフォルト引数）

やっぱり let が気になってしまいます。let をどうにか省略できないものか、、、実はできます！

今回、引数には2つの画像のみが渡ってくることがわかっています。言い換えると引数が3つ以上渡されることはありません。よって f を3つめの引数として定義し f のデフォルト引数として e=>e.naturalWidth/e.naturalHeight を渡しちゃいましょう。

つまりこうです。

export default(a,b,f=e=>e.naturalWidth/e.naturalHeight)=>f(a)-f(b)

やった！66文字。

正攻法の解説は以上です。 ちなみに、natural が2回でてくるので natural をまとめればもっと短くできるかも、と試行錯誤された方も多くいらっしゃいました。私も同じように考えいろいろ試してみたのですが66文字には勝てず、、、もし正攻法で66文字よりも短くできる！という方はぜひ教えてください！

いよいよ次はハック部門の33文字！

ハック部門33文字の解説

まずは33文字のコードをもう一度。

export default()=>9e9<<length+++9

ぱっとみ何をやっているのかわからない謎のコードですね笑 +++ なんてのも実際の業務では見ることはないでしょう。レビューでこれを見たら発狂ものです。

まずはハック部門の方針から解説します。 main.js のテストをよーく眺めてみましょう。

console.assert(compare(a, b) < 0, 'b は a より横長です');
console.assert(compare(b, c) < 0, 'c は b より横長です');
console.assert(compare(c, d) < 0, 'd は c より横長です');
console.assert(compare(d, e) > 0, 'd は e より横長です');
console.assert(compare(e, f) > 0, 'e は f より横長です');
console.assert(compare(f, g) > 0, 'f は g より横長です');
console.assert(compare(g, h) < 0, 'h は g より横長です');
console.assert(compare(h, i) > 0, 'h は i より横長です');
console.assert(compare(i, j) > 0, 'i は j より横長です');
console.assert(compare(j, k) > 0, 'j は k より横長です');
console.assert(compare(k, l) < 0, 'l は k より横長です');
console.assert(compare(l, m) < 0, 'm は l より横長です');
console.assert(compare(m, n) > 0, 'm は n より横長です');
console.assert(compare(n, o) < 0, 'o は n より横長です');
console.assert(compare(o, p) === 0, 'o は p より横長でも縦長でもありません');

あれれ、テストの内容が毎回同じですね！比較する画像の組み合わせも、比較する回数も順番も同じ！
これは、、、

視力検査で前の人が「左」「上」「右」「右」「下」、、、って言ってるのをこっそり暗記して視力を擬似的に UP させるあの技が使えます！！！

つまり、どっちの画像が横長か？なんて一切無視し
「負」「負」「負」「正」「正」「正」「負」「正」「正」「正」「負」「負」「正」「負」「ゼロ」
を返すというとんでもないハックです。

そんなのありかよ！と突っ込みたくなる気持ちはわかりますが JavaScript 的には面白いのでやってみましょう。正攻法よりもむしろこのハックのほうが JavaScript の知識を総動員する必要があって良い頭の体操になりそうです。

「正」「負」「ゼロ」を任意の順番で返す

まずは配列を使って。

let a=[0,-1,1,-1,-1,1,1,1,-1,1,1,1,-1,-1,-1];
export default()=>a.pop()

- の文字（符号）が邪魔なので、pop() した後に -1 引いてみます。

let a=[1,0,2,0,0,2,2,2,0,2,2,2,0,0,0];
export default()=>a.pop()-1

もう66文字！正攻法に並びました。

配列だとコンマ , を使わないといけません。そこで、配列ではなく文字列にして pop() ではなく添字 [] アクセスでひとつずつ取り出します。

let i=0;
export default()=>'000222022200201'[i++]-1

変数宣言を短くする（クロージャ）

またまた let の壁が立ちはだかりました。 よーし、さっき使ったデフォルト引数だ！と思いきや、関数が実行されるたびにインクリメントしていく関係で i は関数の外で宣言しなければなりません。そこで i を「クロージャ（Closure）」に閉じ込めます。

export default(i=>_=>'000222022200201'[i++]-1)(0)

やった！ここから更に1文字減らそうと思えば減らせるのですが、その技はまた後ほど。

さぁ、このアプローチも限界が見えました。ちょっと方針を変えましょう。

符号ビットと左シフト

ここで「符号ビット」という概念に注目です。

「負」「負」「負」「正」「正」「正」「負」「正」「正」「正」「負」「負」「正」「負」「ゼロ」

の値を順番に返していけば良いということは、数値の符号を表す符号ビットが

「1」「1」「1」「0」「0」「0」「1」「0」「0」「0」「1」「1」「0」「1」「0」

で、数値の符号以外の値を示す部分が

「0以外」「0以外」「0以外」「0以外」「0以外」「0以外」「0以外」「0以外」「0以外」「0以外」「0以外」「0以外」「0以外」「0以外」「0」

となれば良いですね！
左シフトしていくと、上記のようになる数値、ビットの並びがあれば、、

64ビット浮動小数点 vs. 32ビット符号付き整数

32ビット符号付き整数で考えると、 要件を満たすビットの並び（2進数表記）は以下です。

0b1110_0010_0011_0100_0000_0000_0000_0000

桁数がわかりやすいように4ビットごとに _ で区切っています。全部で32桁です。

よーし！これを左シフトしていけば、、と思いきや、そうはいきません。 このままでは最上位のビット（32桁目）は「32ビット符号付き整数」の符号ビットとは認識されないのです。

const n = 0b1110_0010_0011_0100_0000_0000_0000_0000; と2進数表記で書くと、なんとなく内部的な型が32ビット符号付き整数になってくれそうな感じがしなくもないですが、そんな事はありません。

const n = 0o34215000000; と 8進数表記で書いても、
const n = 3795058688; と10進数表記で整数ぽく書いても、
const n = 3795058688.0; と10進数表記で小数点付きで書いても、
const n = 0xe2340000; と16進数表記で書いても、
const n = 3.795058688e+9; と指数表記で書いても、
JavaScript 的には違いはありません。（BigInt 表記はまた別ですが！）

上記のいずれも n には（10進数で言うと） 3795058688 という数値が内部的に「64ビット浮動小数点」の型で保持されています。

0b1110_0010_0011_0100_0000_0000_0000_0000 // => 3795058688
0o34215000000 // => 3795058688
3795058688 // => 3795058688
3795058688.0 // => 3795058688
0xe2340000 // => 3795058688
3.795058688e+9 // => 3795058688

表記方法が違っても同じ値と認識されるのは、誰かに1万円を払うときに

• 1万円札1枚でも
• 5千円札2枚でも
• 千円札10枚でも

同じなのと一緒ですね。さすがに1円玉1万枚は困りますが。

32桁目を「32ビット符号付き整数」の符号ビットとして機能させるためには、内部的な型を「64ビット浮動小数点」から「32ビット符号付き整数」に（暗黙的に）切り替えさせる必要があります。 JavaScript のコンテキストによって内部的な型を「64ビット浮動小数点」だったり「32ビット符号付き整数」だったりに切り替えてくれちゃうこの挙動、厄介ですね。 そこで第1問でも登場したテクニック、副作用のない何らかのビット演算をします。

例えばこう。

0b1110_0010_0011_0100_0000_0000_0000_0000 | 0 // => -499908608

はい、これで無事32桁目が32ビット符号付き整数の符号ビットとして機能するようになりました！まさにハック！

これを 1 ずつ左シフトしていけば

「負」「負」「負」「正」「正」「正」「負」「正」「正」「正」「負」「負」「正」「負」「ゼロ」

になりますね！

0b1110_0010_0011_0100_0000_0000_0000_0000 | 0   // =>  -499908608（負）※内部的な型を64ビット浮動小数点から32ビット符号付き整数に暗黙的に切り替えるために副作用のないビット演算をしている
0b1110_0010_0011_0100_0000_0000_0000_0000 <<  1 // =>  -999817216（負）
0b1110_0010_0011_0100_0000_0000_0000_0000 <<  2 // => -1999634432（負）
0b1110_0010_0011_0100_0000_0000_0000_0000 <<  3 // =>   295698432（正）
0b1110_0010_0011_0100_0000_0000_0000_0000 <<  4 // =>   591396864（正）
0b1110_0010_0011_0100_0000_0000_0000_0000 <<  5 // =>  1182793728（正）
0b1110_0010_0011_0100_0000_0000_0000_0000 <<  6 // => -1929379840（負）
0b1110_0010_0011_0100_0000_0000_0000_0000 <<  7 // =>   436207616（正）
0b1110_0010_0011_0100_0000_0000_0000_0000 <<  8 // =>   872415232（正）
0b1110_0010_0011_0100_0000_0000_0000_0000 <<  9 // =>  1744830464（正）
0b1110_0010_0011_0100_0000_0000_0000_0000 << 10 // =>  -805306368（負）
0b1110_0010_0011_0100_0000_0000_0000_0000 << 11 // => -1610612736（負）
0b1110_0010_0011_0100_0000_0000_0000_0000 << 12 // =>  1073741824（正）
0b1110_0010_0011_0100_0000_0000_0000_0000 << 13 // => -2147483648（負）
0b1110_0010_0011_0100_0000_0000_0000_0000 << 14 // =>           0（ゼロ）

あ！初回、32ビット符号付き整数にするための副作用のないビット演算 | 0 を << 0 にすると都合が良さそうです。

0b1110_0010_0011_0100_0000_0000_0000_0000 << 0  // =>  -499908608（負）

つまり、

0b1110_0010_0011_0100_0000_0000_0000_0000 <<  0 // =>  -499908608（負）※内部的な型を64ビット浮動小数点から32ビット符号付き整数に暗黙的に切り替えるために副作用のないビット演算をしている
0b1110_0010_0011_0100_0000_0000_0000_0000 <<  1 // =>  -999817216（負）
0b1110_0010_0011_0100_0000_0000_0000_0000 <<  2 // => -1999634432（負）
0b1110_0010_0011_0100_0000_0000_0000_0000 <<  3 // =>   295698432（正）
0b1110_0010_0011_0100_0000_0000_0000_0000 <<  4 // =>   591396864（正）
0b1110_0010_0011_0100_0000_0000_0000_0000 <<  5 // =>  1182793728（正）
0b1110_0010_0011_0100_0000_0000_0000_0000 <<  6 // => -1929379840（負）
0b1110_0010_0011_0100_0000_0000_0000_0000 <<  7 // =>   436207616（正）
0b1110_0010_0011_0100_0000_0000_0000_0000 <<  8 // =>   872415232（正）
0b1110_0010_0011_0100_0000_0000_0000_0000 <<  9 // =>  1744830464（正）
0b1110_0010_0011_0100_0000_0000_0000_0000 << 10 // =>  -805306368（負）
0b1110_0010_0011_0100_0000_0000_0000_0000 << 11 // => -1610612736（負）
0b1110_0010_0011_0100_0000_0000_0000_0000 << 12 // =>  1073741824（正）
0b1110_0010_0011_0100_0000_0000_0000_0000 << 13 // => -2147483648（負）
0b1110_0010_0011_0100_0000_0000_0000_0000 << 14 // =>           0（ゼロ）

これをコードにすると、

export default(i=>_=>0b1110_0010_0011_0100_0000_0000_0000_0000<<i++)(0)

桁数をわかりやすくするために入れていた区切り文字 _ を取ると、

export default(i=>_=>0b11100010001101000000000000000000<<i++)(0)

だんだん短くなってきました。

0b11100010001101000000000000000000 の文字数が多いので、これをどうにか短くする事を考えます。 いろんな表記でどれだけ短くなるかを比較しましょう。

数値表記を短くする

0b11100010001101000000000000000000 //（2進数表記）
'0o' + 0b11100010001101000000000000000000.toString(8) // => 0o34215000000（8進数表記）
0b11100010001101000000000000000000.toString(10) // => 3795058688（10進数表記）
'0x' + 0b11100010001101000000000000000000.toString(16) // => 0xe2340000（16進数表記）
0b11100010001101000000000000000000.toExponential() // => 3.795058688e+9（指数表記）

どの表記も長い！
ちょっと考え方を変えましょう。

0b11100010001101000000000000000000 << 0 は
0b11100010001101 の後に 000000000000000000 つまり 0 が18個ついている！

言い換えると、

0b11100010001101000000000000000000 << 0 は
0b11100010001101 を18回左シフトしたものだ！

ということは
0b11100010001101 << 18 だ！！！

と考えるのはどうでしょうか？
そうすれば 0 の数を節約できます！が、実際に試してみると、、

export default(i=>_=>0b11100010001101<<(i++)+18)(0)

あれれ！最後のテスト、つまり0 を返すべきテストだけ通らない！！ なぜでしょう？

一つずつ調べていくと、、、

0b11100010001101 << 18 // =>  -499908608
0b11100010001101 << 19 // =>  -999817216
0b11100010001101 << 20 // => -1999634432
0b11100010001101 << 21 // =>   295698432
0b11100010001101 << 22 // =>   591396864
0b11100010001101 << 23 // =>  1182793728
0b11100010001101 << 24 // => -1929379840
0b11100010001101 << 25 // =>   436207616
0b11100010001101 << 26 // =>   872415232
0b11100010001101 << 27 // =>  1744830464
0b11100010001101 << 28 // =>  -805306368
0b11100010001101 << 29 // => -1610612736
0b11100010001101 << 30 // =>  1073741824
0b11100010001101 << 31 // => -2147483648
0b11100010001101 << 32 // =>       14477（あれ！ゼロになるはず！）

最後 0 になるはずが 14477 になっちゃてます！ 32回左シフトすれば全部の桁が 0 になるはずなのに！

0b11100010001101 << 32 // => 14477

原因は、、、もうおわかりですね！

0b11100010001101 << 32

は

0b11100010001101 << (32%32)

つまり

0b11100010001101 << 0

と同じです。仕様的に。

n を正の整数とした時

(0b11100010001101 << n) === (0b11100010001101 << n%32)

です。

日本語版の MDN には（2024/6/14 現在）記述が見当たりませんでしたが、 英語版の MDN にはしっかり以下のように書いてありますね！

The right operand will be converted to an unsigned 32-bit integer and then taken modulo 32, so the actual shift offset will always be a positive integer between 0 and 31, inclusive. For example, 100 << 32 is the same as 100 << 0 (and produces 100) because 32 modulo 32 is 0.

というわけで、最後のテストで左シフトする回数が32未満になるよう、

0b11100010001101000000000000000000 << 0 は

0b11100010001101 の後に 000000000000000000 つまり 0 が18個ついている！
と考えるのではなく、
0b111000100011010 の後に 00000000000000000 つまり 0 が17個ついている！

言い換えると、

0b11100010001101000000000000000000 << 0 は
0b111000100011010 を 17回左シフトしたものだ！

つまり、
0b111000100011010 << 17 だ！！！と考えましょう。

export default(i=>_=>0b111000100011010<<(i++)+17)(0)

今度はテストに通りました！

ここで、(i++)+17 の () は「後置インクリメント演算子」++ と「単項プラス演算子」+ の優先順位の関係から、省略できますね！

export default(i=>_=>0b111000100011010<<i+++17)(0)

+++ がまるで新しい演算子のようにも見えて違和感しか無いですがバッチリ動いてます！

数値表記を短くする

0b111000100011010 もまだ長いのでもっと短く表記できないか試しましょう。またいろいろな表記を比較します。

0b111000100011010 // 2進数表記
'0o' + 0b111000100011010.toString(8) // => 0o70432（8進数表記）
0b111000100011010.toString(10) // => 28954（10進数表記）
'0x' + 0b111000100011010.toString(16) // => 0x711a（16進数表記）
0b111000100011010.toExponential() // => 2.8954e+4（指数表記）

上記の中では

• 10進数表記 28954

が5文字で一番文字数が短いですね！

export default(i=>_=>28954<<i+++17)(0)

やった！一気に短くなりました。

念の為 28954 を素因数分解してみましょうか。

残念、、、あまり短くできそうにありません。

?**? とか ?+?? とかでも短くは書けなそうです。たぶん。

ちょっとここで考え方を変えましょう。

要件を満たす数値は実はたくさんある

以下をご覧ください。※ ? は 0 か 1 のいずれかという意味で使っています

0b111000100011010 << 17 // => -499908608
0b?_111000100011010 << 17 // => -499908608
0b??_111000100011010 << 17 // => -499908608
0b???_111000100011010 << 17 // => -499908608
0b????_111000100011010 << 17 // => -499908608
0b?????_111000100011010 << 17 // => -499908608
0b??????_111000100011010 << 17 // => -499908608
0b???????_111000100011010 << 17 // => -499908608
0b????????_111000100011010 << 17 // => -499908608
0b?????????_111000100011010 << 17 // => -499908608
0b??????????_111000100011010 << 17 // => -499908608
0b???????????_111000100011010 << 17 // => -499908608
...

17回左シフトするので、111000100011010 の左にはどんなビットが並んでいても関係ありません。

さらに以下もご覧ください。

111000100011010 の右には、0 が 17個以下であれば何個並んでいても左シフトの初期値で吸収できます。

0b111000100011010 << 17 // => -499908608
0b111000100011010_0 << 16 // => -499908608
0b111000100011010_00 << 15 // => -499908608
0b111000100011010_000 << 14 // => -499908608
0b111000100011010_0000 << 13 // => -499908608
0b111000100011010_00000 << 12 // => -499908608
0b111000100011010_000000 << 11 // => -499908608
0b111000100011010_0000000 << 10 // => -499908608
0b111000100011010_00000000 << 9 // => -499908608
0b111000100011010_000000000 << 8 // => -499908608
0b111000100011010_0000000000 << 7 // => -499908608
0b111000100011010_00000000000 << 6 // => -499908608
0b111000100011010_000000000000 << 5 // => -499908608
0b111000100011010_0000000000000 << 4 // => -499908608
0b111000100011010_00000000000000 << 3 // => -499908608
0b111000100011010_000000000000000 << 2 // => -499908608
0b111000100011010_0000000000000000 << 1 // => -499908608
0b111000100011010_00000000000000000 << 0 // => -499908608

まとめると

0b?????????????????_111000100011010  << 17 // => -499908608
0b????????????????_111000100011010_0 << 16 // => -499908608
0b???????????????_111000100011010_00 << 15 // => -499908608
0b??????????????_111000100011010_000 << 14 // => -499908608
0b?????????????_111000100011010_0000 << 13 // => -499908608
0b????????????_111000100011010_00000 << 12 // => -499908608
0b???????????_111000100011010_000000 << 11 // => -499908608
0b??????????_111000100011010_0000000 << 10 // => -499908608
0b?????????_111000100011010_00000000 <<  9 // => -499908608
0b????????_111000100011010_000000000 <<  8 // => -499908608
0b???????_111000100011010_0000000000 <<  7 // => -499908608
0b??????_111000100011010_00000000000 <<  6 // => -499908608
0b?????_111000100011010_000000000000 <<  5 // => -499908608
0b????_111000100011010_0000000000000 <<  4 // => -499908608
0b???_111000100011010_00000000000000 <<  3 // => -499908608
0b??_111000100011010_000000000000000 <<  2 // => -499908608
0b?_111000100011010_0000000000000000 <<  1 // => -499908608
0b111000100011010_00000000000000000  <<  0 // => -499908608

111000100011010 の前（左）にどんなビット並んでいても、
111000100011010 の後（右）に0がたくさんついていても、
何回か左シフトすれば -499908608 になりますね！

なお、 32桁目の符号ビットが 0、すなわち正の数の場合、

0b0????????????????_111000100011010 
0b0???????????????_111000100011010_0
0b0??????????????_111000100011010_00
0b0?????????????_111000100011010_000
0b0????????????_111000100011010_0000
0b0???????????_111000100011010_00000
0b0??????????_111000100011010_000000
0b0?????????_111000100011010_0000000
0b0????????_111000100011010_00000000
0b0???????_111000100011010_000000000
0b0??????_111000100011010_0000000000
0b0?????_111000100011010_00000000000
0b0????_111000100011010_000000000000
0b0???_111000100011010_0000000000000
0b0??_111000100011010_00000000000000
0b0?_111000100011010_000000000000000
0b0_111000100011010_0000000000000000

上記の数値は 0b00000000000000000_111000100011010（10進数表記で 28954）以上になりますね！

もし、 32桁目の符号ビットが 1、すなわち負の数であれば、

0b1????????????????_111000100011010 
0b1???????????????_111000100011010_0
0b1??????????????_111000100011010_00
0b1?????????????_111000100011010_000
0b1????????????_111000100011010_0000
0b1???????????_111000100011010_00000
0b1??????????_111000100011010_000000
0b1?????????_111000100011010_0000000
0b1????????_111000100011010_00000000
0b1???????_111000100011010_000000000
0b1??????_111000100011010_0000000000
0b1?????_111000100011010_00000000000
0b1????_111000100011010_000000000000
0b1???_111000100011010_0000000000000
0b1??_111000100011010_00000000000000
0b1?_111000100011010_000000000000000
0b1_111000100011010_0000000000000000
0b111000100011010_00000000000000000 

同様に、上記の数値は 0b11111111111111111_111000100011010（10進数表記で -3814）以下になります！

そして、これらの数値を2進数表記で表してももちろん良いですが、 8進数表記でも、10進数表記でも、16進数表記でも、はたまた指数表記でも、一番文字数が短く書ければどんな表記でも（値が同じであれば）良いわけです。

例えば、以下のコード

export default(i=>_=>0b111000100011010<<i+++17)(0)

は

0b111000100011010 の左を全部 1 で埋めて

export default(i=>_=>0b11111111111111111_111000100011010<<i+++17)(0)

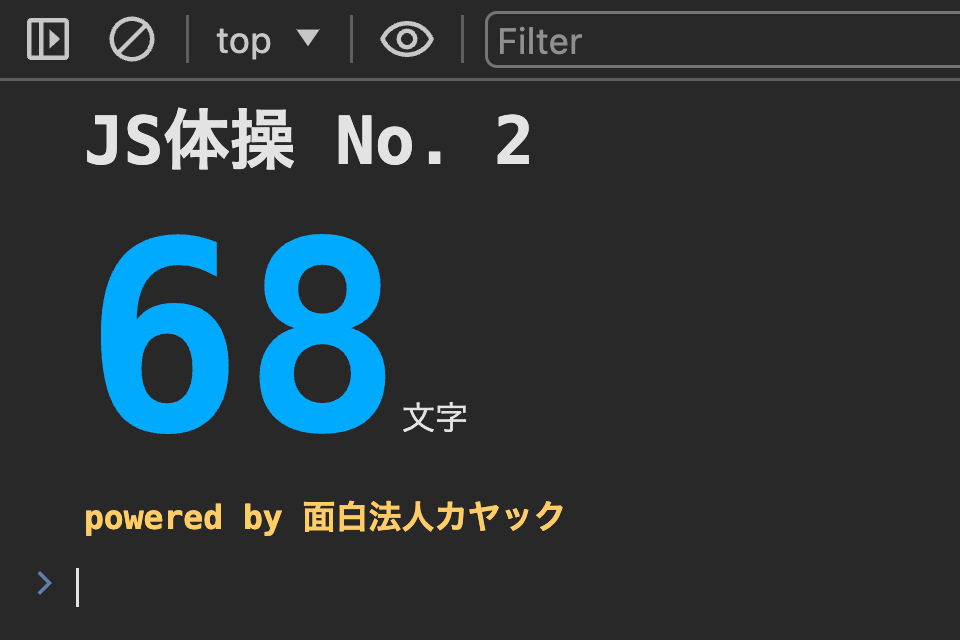
としても良いですし、

0b11111111111111111_111000100011010（32ビット符号付き整数の想定）を 10進数で -3814 と書いて

export default(i=>_=>-3814<<i+++17)(0)

でも良いわけです。

28954以上もしくは-3814以下の数値で、上述の要件を満たし、且つ5文字未満で書ける可能性がある表記方法は、、、おそらく指数表記のみではないでしょうか？たぶん。
（上述の要件を満たすかは別として、28954以上もしくは-3814以下で、且つ指数表記で5文字未満で書ける数値の例は 3e4 や 29e3、-4e3 です）

もし

export default(i=>_=>◯e◯<<i+++◯)(0)

みたいに書けたら一気に文字数を減らせますね！

つまり、

• N 回左シフトしたら -499908608 になる（N の桁数は少ないほうがいい）
• 指数表記で5文字以下※で表せる

※「未満」ではなく「以下」なのは5文字でも左シフトの回数が1桁にできるかもしれないので

という都合の良い数値が見つかれば、1文字（指数表記で1文字減らせるかも）から3文字（指数表記で2文字減らせるかも＆ N が2桁から1桁になるかも）は短くできそうです！

条件に合う数値を探す

そんな数値を人間の手で探すのは大変なので今回は JavaScript に探してもらいましょう。 例えばこんなざっくりコードで。

const N_MAX = 999;// `999e9` のような指数表記5文字以下で表せる数値を探したいので
const M_MAX = Math.ceil(Math.log10(Number.MAX_VALUE));

const map = new Map;

let minLength = 5;// `999e9` のような指数表記5文字以下で表せる数値を探したいので
let m = 1;

function check(str) {
  const len = str.length;

  if (len <= minLength) {
    minLength = len;

    const arr = map.get(minLength) || [];

    arr.push(str);
    map.set(minLength, arr);
  }
}

function search() {
  for (let n = 1; n < N_MAX; ++n) {
    const rgx = /1110001000110100+$/;
    const num = n * 10**m;

    // 正
    {
      const bin = num.toString(2);

      if (rgx.test(bin)) {
        check(`${n}e${m}`);
      }
    }

    // 負（桁数オーバーとかはチェックしてません）
    {
      const bin = (num - 1).toString(2).replace(/./g, bit => '10'[bit]).padStart(32, '1');

      if (rgx.test(bin)) {
        check(`-${n}e${m}`);
      }
    }
  }

  console.log(`Searching... (${(m * 100 / M_MAX).toFixed(2)}%) ${minLength}文字 ${map.get(minLength) || '-'}`);

  if (++m < M_MAX) {
    setTimeout(search, 100);
  } else {
    console.log('Complete!');
    console.log(`最短文字数: ${minLength}文字\n数値: ${map.get(minLength)?.join()}`)
    console.dir(map);
  }
}

search();

ブラウザが固まらないようにインターバルをはさんで探すようにしてます。（もちろんブラウザではなく Node.js 上で実行してもよいですね！）

実行してしばらく待つと、、、

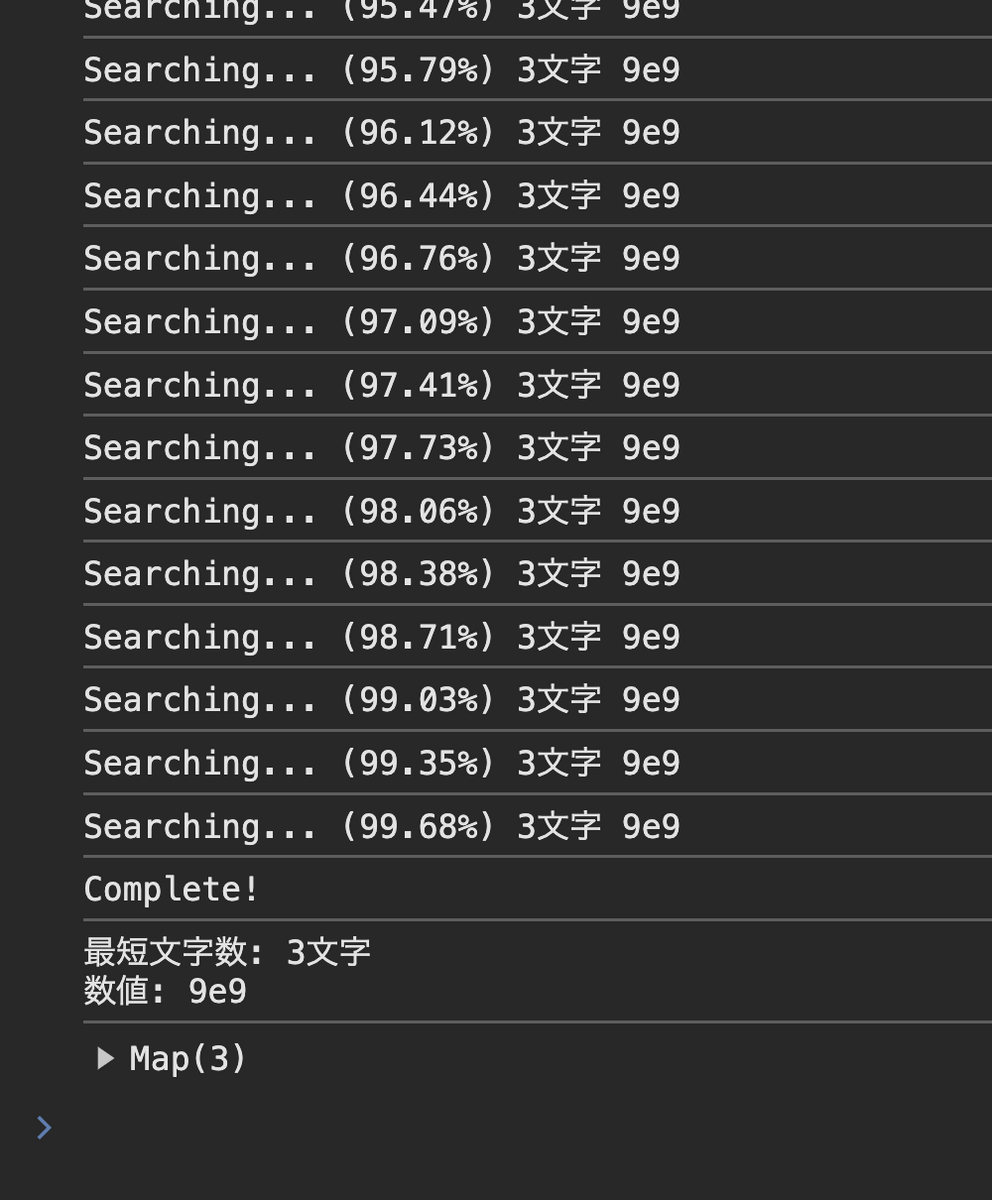
9e9 ！！！！！！！ 短い！！！

9e9 を2進数表記に直すと

'0b' + 9e9.toString(2) // => 0b1000011000011100010001101000000000

なので

9e9<<9 で 0b111000100011010<<17 と同じになりますね！

9e9<<9 === 0b111000100011010<<17 // => true

ということで

export default(i=>_=>9e9<<i+++9)(0)

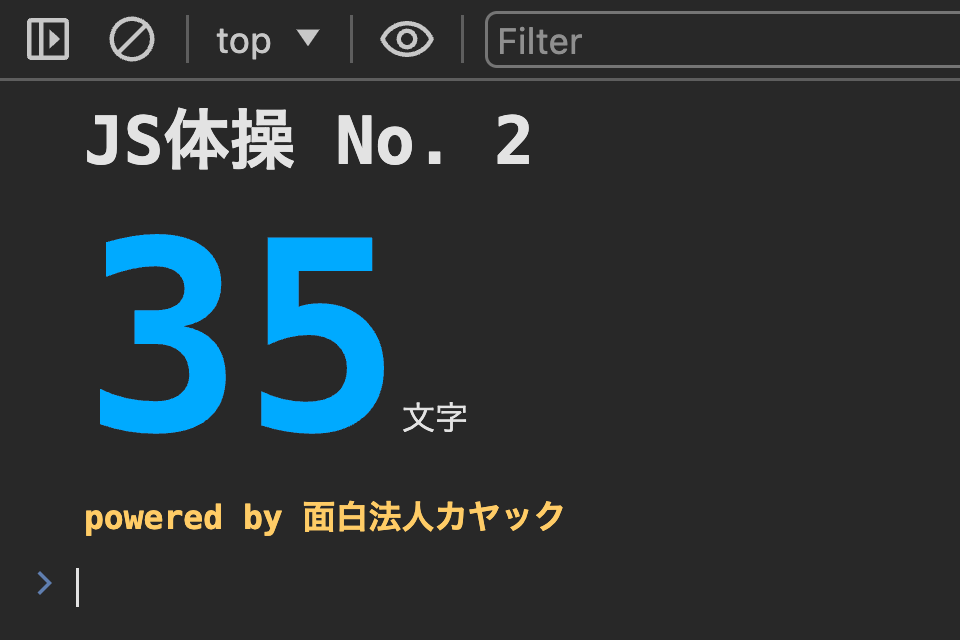
短くなってきた！！
でもまだまだあきらめません！

変数宣言を短くする（クロージャ + 暗黙の型変換）

i に 0 を渡している部分 (0) を短くしたいです。 0 を直接渡すのではなく 0 に変換できる何かを渡すことで短くできないでしょうか？

例えば空の配列 []。
空の配列 [] は数値に変換すると 0 になりますね。

+[] // => 0

export default(i=>_=>9e9<<i+++9)([])

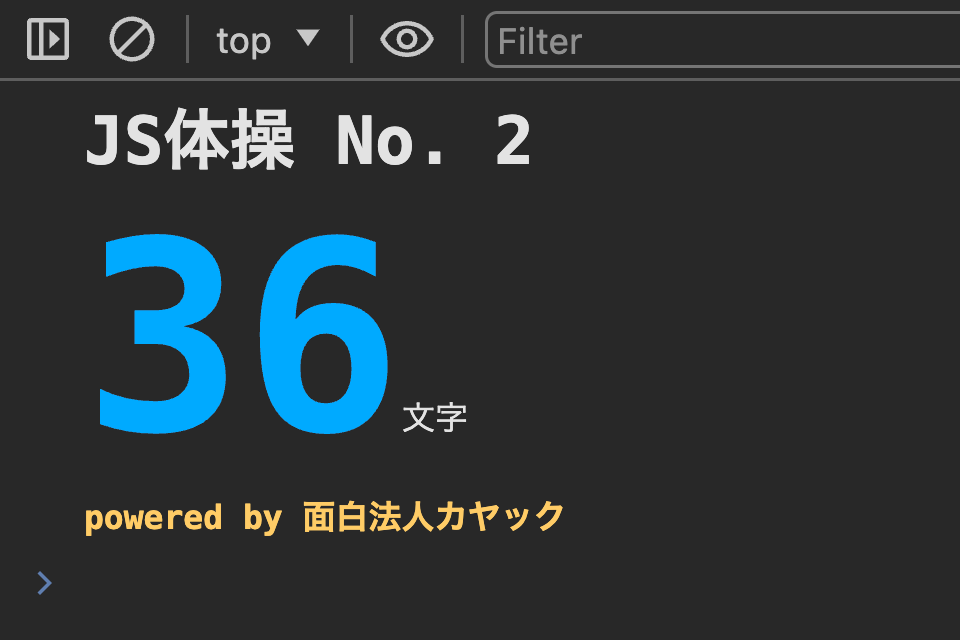
1文字増えた、、 長くなっとるやないかーい！と思ったあなた、ここからが面白いところです！

今度は空の配列 [] を直接ではなく間接的に渡してみましょう。 例えばこうです。

export default(i=>_=>9e9<<i+++9)``

2文字減った！

これはテンプレートリテラルとタグ関数の仕様を利用しています。 それらの説明は過去の記事で紹介しているのでここでは割愛します。

techblog.kayac.com

さて、34文字まで減らせました。もう限界でしょうか。。

34文字って（後日別の記事で紹介予定の）console.assert() を上書きするチートと同じじゃん！こんなに苦労したのに楽勝チートと同じ文字数なんてやってられるか！と思ったあなた、もう少しご辛抱ください。

クロージャを使う方針ではこれ以上は短くできそうにありません。
厳格モード（Strict Mode）でさえなければ、、
i=0 を let 無しで暗黙的にグローバル変数として宣言できれば、、

i=0;export default()=>9e9<<i+++9 // => Uncaught ReferenceError: i is not defined

ん？
グローバル変数？？

変数名がなるべく短くて、再代入できて、値が数値もしくは数値に変換できるような都合の良い既存のグローバル変数があれば、、、

変数宣言を短くする（既存のグローバル変数の利用）

そんな都合の良いグローバル変数がないか、これまた JavaScript で探してみましょう。

Object.keys(window).filter(key => !isNaN(+window[key])).sort((a, b) => a.length - b.length).map(key => [key, window[key], +window[key]])

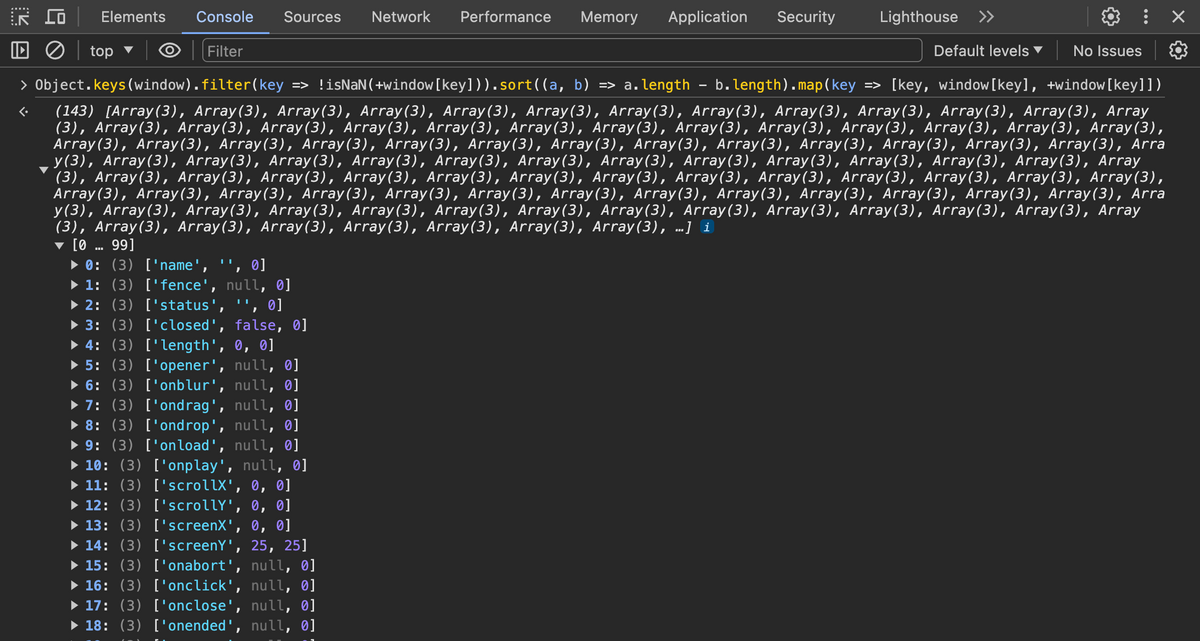
window.name ！！！

早速使ってみましょう

export default()=>9e9<<name+++9

31文字！！！！めちゃ短くなった！！！ 今度こそゴールだ！！と思いきや、、、

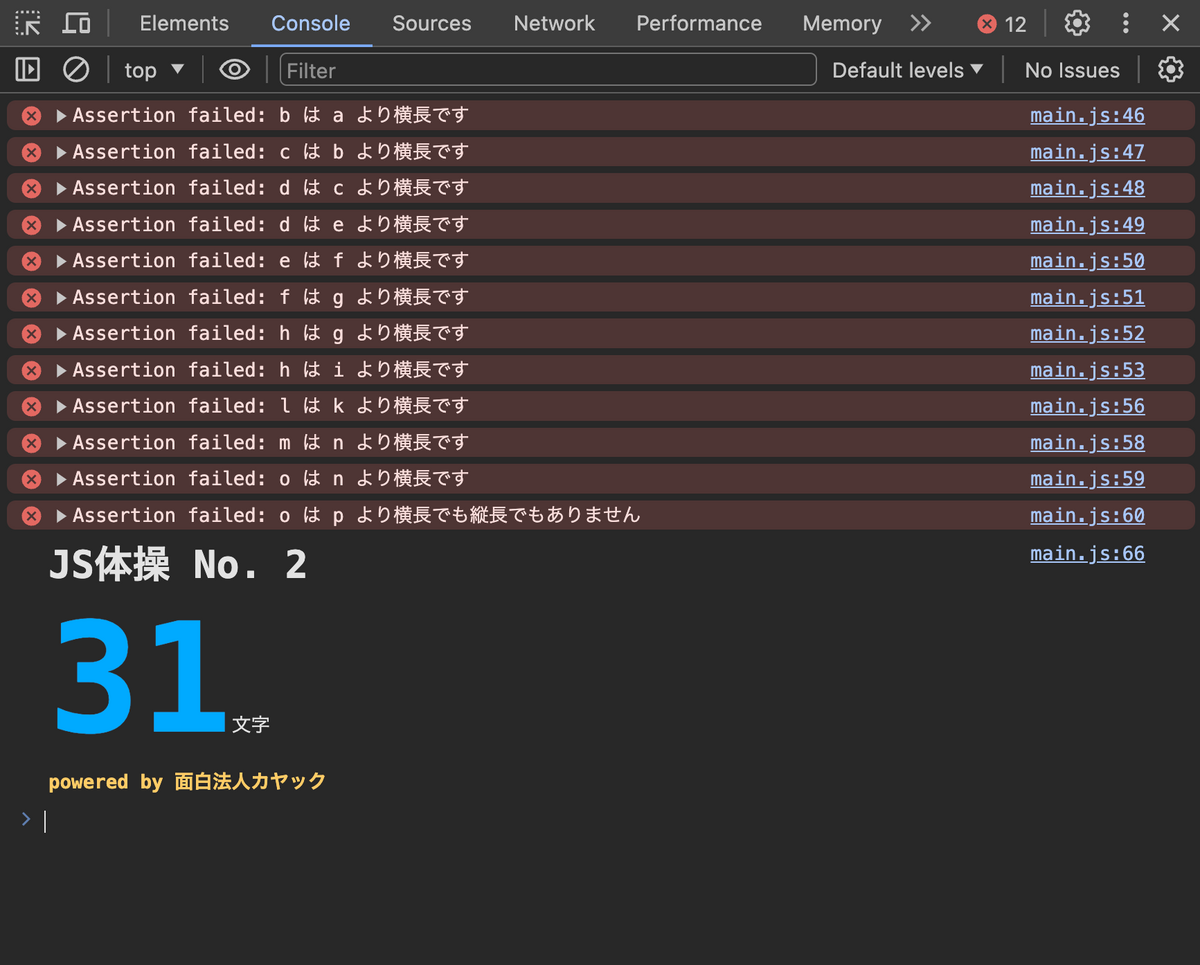
リロードしたらなぜかエラーが。 コードは変えてないはずなのに。

はい、なぜこうなるかはwindow.nameの仕様を読むとわかります！ window.name は本来はウィンドウ（タブ）の名前を格納するためのプロパティであり、ウィンドウ（タブ）が閉じられない限り値が保持されてしまいます。（「しまいます」というのもおかしいですが）よって、最初の一回目は 0 から 15 までインクリメントされて無事すべてのテストに合格して終了しますが、リロードすると前回の 15 が（文字列 '15' として）保持されているので、0 からではなく 15 からインクリメントされてしまいます。なんてこった！

つまりウィンドウ（タブ）を開いた直後の一回しか動かない極悪仕様。 さすがにこの31文字を最短文字数とすると暴動が起きそうなのでやめておきます。すでに起きてるかもですが。

4文字の window.name は諦めて、 5文字の window.fence はどうでしょうか！

export default()=>9e9<<fence+++9

残念！window.fence は読み取り専用でした。さらにまだ Experimental のようです。

では次の候補の window.length はどうでしょう？

export default()=>9e9<<length+++9

やった！何度リロードしても問題なし！！
34文字で console.assert() を上書きするチートにも勝ちました！
MDN によるとwindow.length は

ウィンドウにおけるフレーム（<frame> か <iframe> 要素のいずれか）の数を返します。

とあります。今回の問題では <frame> も <iframe> も使っていないので window.length は 0 です。もし Google Analytics とかアクセス解析のコードを仕込んでいたら 1 とかになるかもしれませんね！そして <frame> か <iframe> が9個ある環境なら、、、+9 を省略し2文字減らせますね笑（ちなみに window.length は読み取り専用じゃないのが驚愕でした。。。）

ようやく長い旅が終わりました。おつかれさまでした。 これ以上短くするのはおそらく無理でしょう。いや、無理じゃないかもしれません。 もし、もっと短くできた！という方がいればぜひ教えてください！

縦横比を比較する応用例

ランダムなサイズの表示領域に、画像をピッタリ収まるように配置するサンプルを

• Canvas2D 版
• WebGL 版
• CSS 版
• DOM 版

の4種類の方法で作ってみました。

表示領域は赤く塗りつぶされています。

画像は以下の3種類、横長／縦長／正方形のものからランダムで選ばれます。

CodePen のサンプルコードを用意しましたので、各サンプル右下の「Rerun」ボタンを押し、表示領域のサイズや画像の種類を切り替えてみてください。

Canvas2D 版

See the Pen 『JS体操』第2問 応用サンプル Canvas2D 版 by Tohl SMALLFIELD (@tsmallfield) on CodePen.

まさに正攻法のロジックを使用しています。

• 画像のほうが表示領域よりも横長であれば、画像の横幅を表示領域の横幅にピッタリ合わせる
• 画像のほうが表示領域よりも縦長であれば、画像の縦幅を表示領域の縦幅にピッタリ合わせる
• 画像も表示領域も同じくらい横長であれば、画像の横幅も縦幅も表示領域にピッタリ合わせる

というロジックです。

// 画像のほうが横長
if (cvsAspectRatio < imgAspectRatio) {
  const imgDestWidth  = STAGE_WIDTH;
  const imgDestHeight = imgDestWidth / imgAspectRatio;

  const imgDestX = 0;
  const imgDestY = (STAGE_HEIGHT - imgDestHeight) / 2;

  ctx.drawImage(img, imgDestX, imgDestY, imgDestWidth, imgDestHeight);

// 表示領域（キャンバス）のほうが横長
} else if (imgAspectRatio < cvsAspectRatio) {
  const imgDestHeight = STAGE_HEIGHT;
  const imgDestWidth  = imgDestHeight * imgAspectRatio;

  const imgDestX = (STAGE_WIDTH - imgDestWidth) / 2;
  const imgDestY = 0;

  ctx.drawImage(img, imgDestX, imgDestY, imgDestWidth, imgDestHeight);

// 表示領域（キャンバス）も画像も同じくらい横長
} else {
  const imgDestWidth  = STAGE_WIDTH;
  const imgDestHeight = STAGE_HEIGHT;

  const imgDestX = 0;
  const imgDestY = 0;

  ctx.drawImage(img, imgDestX, imgDestY, imgDestWidth, imgDestHeight);
}

WebGL 版

See the Pen 『JS体操』第2問 応用サンプル WebGL 版 by Tohl SMALLFIELD (@tsmallfield) on CodePen.

こちらも正攻法のロジックで条件分岐しています。

WebGL では 頂点シェーダで gl_Position にわたす座標は最終的には正規化する必要がありますね。 Three.js などのライブラリを使う場合は表示領域（画面）の縦横比関連の変換は「プロジェクション行列（Projection Matrix）」がやってくれますが 本サンプルでは説明のため「プロジェクション行列」という概念は使わずなるべく素の状態にしています。

• Z軸は無視できるようにしている（つまり2次元）
• 表示領域の座標（クリップ座標）は（, （ ） に正規化されている）
• 初期状態で表示領域いっぱい（, , ）に広がる板ポリが一枚ある
• 板ポリのサイズを表示領域の縦横比、画像の縦横比に応じて変えたい（X軸方向のスケール or Y軸方向のスケールを変えたい）
• 領域の縦横比はユニフォーム変数 cvsAspectRatio で渡ってくる
• 画像の縦横比はユニフォーム変数 imgAspectRatio で渡ってくる

という仕様です。

このような条件下だと、Canvas2D 版と比較してシンプルなロジックで書けます！ 「『縦横比』と『縦横比』の比」という概念が登場して面白いですね！「縦横比」の比は「縦横比比」とでも言うのでしょうか？
※ 以下のコードは JavaScript ではなく GLSL（頂点シェーダ）です。

attribute vec2 pos, uv;
uniform float cvsAspectRatio, imgAspectRatio;
varying vec2 vUv;

void main() {
  vec2 p = pos;

  // 画像のほうが横長
  if (cvsAspectRatio < imgAspectRatio) {
    p.y *= cvsAspectRatio / imgAspectRatio;

  // 表示領域（キャンバス）のほうが横長
  } else if (imgAspectRatio < cvsAspectRatio) {
    p.x *= imgAspectRatio / cvsAspectRatio;

  // 表示領域（キャンバス）も画像も同じくらい横長
  } else {
    ; // 何もしなくて良い
  }

  vUv = uv;
  gl_Position = vec4(p, 0, 1);
}

CSS 版

See the Pen 『JS体操』第2問 応用サンプル CSS 版 by Tohl SMALLFIELD (@tsmallfield) on CodePen.

一応 CSS 版も。
縦横比なんて一切気にせず、background-size: contain; で一発ですね！

DOM 版

See the Pen 『JS体操』第2問 応用サンプル DOM 版 by Tohl SMALLFIELD (@tsmallfield) on CodePen.

そして DOM 版も。
こちらも縦横比なんて一切気にせず、object-fit: contain; で（対応しているブラウザなら）一発です！

まとめ

今回も最後まで読んでいただき、ありがとうございます！

正攻法 66文字

export default(a,b,f=e=>e.naturalWidth/e.naturalHeight)=>f(a)-f(b)

ハック部門 33文字

export default()=>9e9<<length+++9

「正攻法」と「ハック部門」の解説、いかがでしたか？ 特に「ハック部門」では、想定外の解法もあり出題者の私もとても勉強になりました。

第2問では（第1問とは違い）文字数の目安を当初「200文字」としか提示しなかったので、先が見えない、終わりのない困難な戦いだったのではないでしょうか？ もうこれ以上短くするのは無理でしょ！とか、この方法より短くできるはずはないはず！と思ってしまったり、コードゴルフはそんな自分との孤独な戦いでもあります。

もちろん、本記事でご紹介した正攻法の66文字やハック部門の33文字もこれ以上短くできない、とは限りません。特にハック部門はまだまだいけるかも？締め切りは過ぎましたがフォームでの回答はいつでも可能、大歓迎です。もしもっと短くできた！という人はぜひ教えてください。とても喜びます。

『JS体操』はその名の通り、きつい筋トレでもなくピリピリした競技でもなく、ゆるーい頭の体操を目指しています。 だからこそいろんなアプローチで解けるような問題をこれからも出題していく予定です。 ぜひ頭を柔らか〜くして楽しんでください！

禁断の「チート部門」3種は後日別の記事でお届け予定です。

そして第1問の面白解答編、おまたせしておりますがこちらも近々公開いたします！ お楽しみに！

お知らせ

次回以降の「解説ブログ」や「JS体操の問題」のお知らせが気になる方はこちらにご登録ください。
公開次第、ご連絡します！

hubspot.kayac.com

『JS体操』第1問、まだ挑戦していない！という方はぜひ

hubspot.kayac.com

先日、Perl のコードゴルフコンテストもカヤック主催で開催されました。
こちらも面白いのでぜひご覧ください！

techblog.kayac.com

そして、カヤックではコードゴルフが大好きな新卒＆中途エンジニアも募集しています！

www.kayac.com www.kayac.com