ベクトルを3D空間で回す

画面写真をクリックするとWebGLビルドに飛びます。 ソースコードはgithubに置いてあります。

こんにちは。技術部平山です。

今日は、球面に点を散らす方法を使って、 3D空間でベクトルをいろんな方向に曲げてみます。 これができて初めて、「ビームが敵に当たると火花が散る」 といったことができるようになります。

なお、今回も高校数学を使います。ほぼベクトルと幾何です。 ベクトルと幾何がある程度使えないと、 3Dゲームを作る際にはかなり選択肢が狭められてしまいます。 「数学的な処理は自分では書かない。アセットストアとgoogleで勝負」 というスタンスもあるでしょうけれども、 まあこの記事に辿りつかれたのも何かの縁でしょう。 少し眺めていって頂ければと思います。

サンプル

サンプルは、(0,0,0)から広がりのあるビームの束を 発射するものです。 ビームの中心軸はテキトーに回転し、 それぞれのビームはある程度の広がりをもって散ります。 ビームの描画はLineRendererです。

散り具合はスライダーで設定でき、 これは前回やった「分布にsinφの累乗を掛ける、その累乗」の値として使っています。

さて、ここで必要な処理は何でしょうか。

まずベクトルを散らす所から

まず、前回ご紹介した所をやってしまいましょう。 前回作った「半球に分布する点を生成する関数」を用意します。 二つの角度が出てくる関数ならなんでもいいのですが、 サンプルでは散り具合を調整できるバージョンを使っています。

public static void GetHemisphericalCosPoweredDistribution(
    out float phi, //φ
    out float theta, //θ
    float power) // 何乗するか。8乗するなら8
{
    theta = Random.Range(-Mathf.PI, Mathf.PI);
    var r = Random.Range(0f, 1f);
    var powered = Mathf.Pow(r, 1f / (power + 1f));
    phi = Mathf.Acos(powered);
}

前回Asinだった所がAcosになっているのは、 今回は一般的なやり方に合わせてφはz軸プラス方向を起点としているからです。

中心軸ベクトルを二つの角度を使って回転する

では回すベクトルを用意しましょう。ビームの中心軸ベクトルです。

ここで、もし普通にUnity的な作り方をしていれば、 ビームの発射方向を表すGameObjectが存在しているでしょう。 そうならば、そのGameObjectが持つTransformの forward を取り出せば、ワールド座標における前方向ベクトルが取れます。 これを中心軸として使えば良いでしょう。

しかし今回のサンプルでは、「ビーム砲」的なGameObjectがありません。 以前ご紹介したビームがたくさん出るサンプルでも、 ビームごとにGameObjectを置かない実装でした。

中心軸ベクトルは単なるVector3でして、Update()にて、

float t = Time.time * 3;
beamAxis.x = Mathf.Cos(t) * Mathf.Cos(t * 1.3f);
beamAxis.y = Mathf.Cos(t) * Mathf.Sin(t * 1.3f);
beamAxis.z = Mathf.Sin(t);

こんな感じにテキトーに回したベクトルを作っています。 なので、Transformの機能が使えません。 今回のメインディッシュはこのようにTransformがない場合でも回す方法なのですが、 たぶん大半の方はTransformを使って回せればオーケーでしょう。 そこで、軽くそのやり方も確認しておきます。

Transformがある場合

まずビームの中心軸はTransform.forwardで取れます。

var beamAxis = cannonTransform.forward;

cannonTransform、というものがビーム砲のTransformであるとしました。 このbeamAxisはワールド座標におけるベクトルです。 こうして得たbeamAxisをφとθで回すわけですが、 ワールド座標のまま回すのは簡単ではありません。

何故なら、φやθはローカル座標において、(0,0,1)を回す時の角度 だからです。他の座標系で回す時や、(0,0,1)以外のベクトルを回す時には そのまま使えないのです。

どうなるのかちょっとやってみましょう。

例えばワールド座標系のX軸を軸にして30度回すとします。 砲が真北(Z+)を向いてる時のワールド座標系のX軸は、 砲にとって見れば右側で、 砲が真東(X+)を向いている時は正面です。 北を向いている時に30度回せばビームは下向きになりますが、 砲が東を向いている時に30度回しても、正面方向が軸と一致してしまって 全く変化しません。 砲がどっちを向いているかで結果が違ってしまうのです。

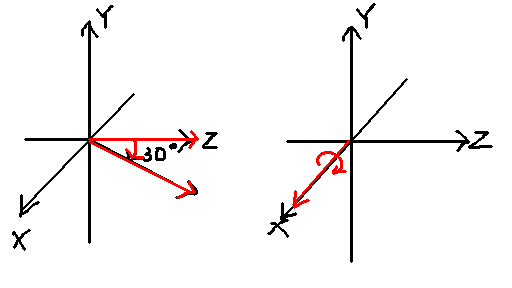
というわけで、ローカル座標で回しましょう。 ローカル座標における正面ベクトルは(0,0,1)ですから、 これをφとθで回します。

極座標からx,y,zへの変換は、

localVector.x = Mathf.Sin(phi) * Mathf.Cos(theta);
localVector.y = Mathf.Sin(phi) * Mathf.Sin(theta);
localVector.z = Mathf.Cos(phi);

で行えます。繰り返しになりますが、前回の記事と違っているのは、φが極起点だからです。 Z+方向が0度で、Z軸と直交したら90度、となるようにφを定義しています。

次にやることは、このベクトルをワールド座標に持っていくことです。 ベクトルを座標変換するには行列を掛ければ良く、 そのための行列はTransformが持っています。 これを使って変換しましょう。

var toWorld = starTransform.localToWorldTransform;
var worldVector = toWorld.MultiplyVector(localVector);

あっさりできましたね。MultiplyPoint()でなくMultiplyVector()を使うので、 間違えないようにしましょう。点とベクトルの区別は大事です。

さて、これで目的は完璧に果たせますので、 それで済む方はこの先を読む必要はありません。 散らす中心方向を向いたTransformを用意しましょう。

Transformがない場合

さて今回のメインディッシュ(でありながらおまけ)です。

Transformがない場合、素の中心軸ベクトル(beamAxis)があるだけです。 これはワールド座標なので、ワールド座標のまま回転せざるを得ません。 先程避けた「ワールド座標のままで回転」をやる必要があるわけです。

まず、角度が二個あって問題が難しいので、一つづつに分割しましょう。 すなわち、 「あるベクトルをある角度回す」という問題をまず解きます。 解けたら、それを使って元の問題を解くことにしましょう。

あるベクトルをある角度回す

何かベクトルvがあって、これを角度θだけ回す、 ということを考えます。

しかし、回すって、どう回すんですかね?

三次元空間においては、回し方が無数にあります。 立っている人が立ったまま回る方法もありますし、 立っている人が倒れるのもまた回転です。

真北(Z+)を向いて立った人が、 立ったまま回るのはY軸回転で、 前や後ろに倒れればX軸回転で、 左や右に倒れればZ軸回転となります。 つまり、回る軸を指定しなければなりません。

ここでは、「よくわからないが軸が与えられている」としましょう。 軸aが与えられていて、それに関して回す、と考えます。

関数の形はこんな感じでしょう。

Vector3 RotateVector(Vector3 v, Vector3 a, float theta);

図を描く

さて、この手の問題を解く時には、数式をこねくり回してもイメージが湧きませんので、 図を書きます。数学は大きく分けて、代数(≒方程式)、幾何(≒図形)、解析(≒微積分)の3分野に分かれるそうで、 問題によってはそのうちの複数の手法が使えたりもしますが、 ベクトルが出てくる類の問題はまず幾何として解くのが楽でしょう。 そして幾何で解くならとにかく図です。 だいたいこんな感じでしょうか。

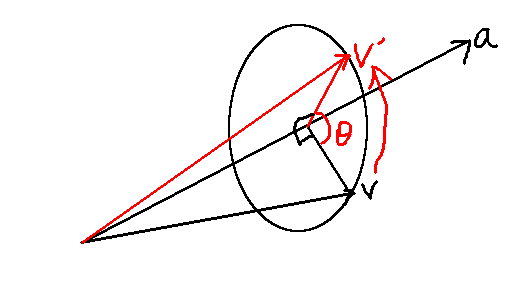
aを軸にしてθだけ回して、vをv'に持ってくるわけです。

まず、立体だと考えるのが面倒で図も描きにくいので、平面の問題にしましょう。 vをa上に射影します。「射影」というのは、 読んで字の通り、「影を落とす」ことです。

vとaだけ写った図を描くと、

という感じです。vとaの交点をO、vの終点をVとして、 Vからaに垂線を引いて、aと交わる所をCとしましょう。 このCを求めるのが「射影」という計算です。 なお、大文字は点で、小文字はベクトルとお考えください。

さて、vとaの角度をαとすると、OからCの長さは、|v|*cos(α)ですから、

C = O + (|v|*cos(α))*a/|a|

と書けますね。式を簡単にしたいので、「aの長さは1」 と決めてしまいましょうか。 そうすると、

C = O + |v|*cos(α)*a

と簡略化できます。ではcos(α)を求めましょう。

内積と角度

ベクトルをいじっている最中にコサインや角度が欲しくなったら、脊髄反射で内積を思い出します。 ベクトルuとvのなす角度θは、

cos(θ) = Dot(u, v) / (|u||v|)

と書けますから、これを使うと、

C = O + |v|*Dot(v, a)*a/(|v||a|)

となります。分子と分母に|v|があるので消してしまいましょう。 さらに、分母にある|a|は1とわかっていますから、これも消えます。

C = O + Dot(v, a)*a

ベクトルcをOからCに向かうベクトルとすれば、 Oを足す必要はなくなるので、

c = Dot(v, a)*a

で終わります。射影を関数化しておきましょうか。

static Vector3 ProjectVector(
    Vector3 v,
    Vector3 axisNormalized)
{
    return Vector3.Dot(v, axisNormalized) * axisNormalized;
}

aは長さが1でないといけないので、引数の名前でそれを強調しておきました。 念を入れるなら、Debug.Assertを使って長さが1くらいであることを確認してもいいですが、 だいぶ遅くなるのでおすすめはしません。

平面の問題として解く

さて、この段階で、C、V、V'を含む平面の問題として考えられます。図を書きましょう。

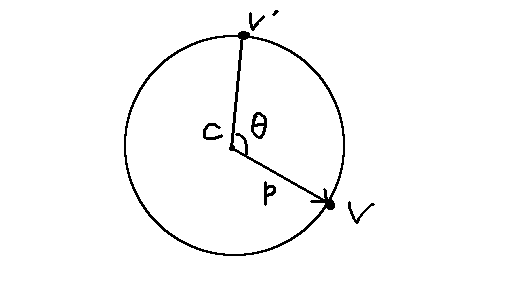
円周上にあるVを、Cを中心にθだけ回してV'を得る、という問題です。 CからVへ向かうベクトルはpとしておきました。 V'をどうやって表せばいいでしょうか。

さて、平面上のあらゆる点は、原点に2つのベクトルの長さをテキトーに調節しつつ足すことで表せます。 例えば(3,1)は、(1,0)に3を掛けたものと、(0,1)に1を掛けたものを足せば作れます。 2つのベクトルに必要な条件は「平行でないこと」だけですが、 二つが直交していると扱いが楽になります。

そこで、pに直交するベクトルqを何らかの手段ででっちあげて、 CにqとpをほどよくブレンドしてV'を作ることを考えましょう。

そうすれば、

V' = C + p*s + q*t

と表せます。sとtは0.2とか0.4とかの数値で、これを求めればV'が求まります。 というわけで、qをでっちあげましょう。 さあ、「直交したベクトルが欲しいな」と思ったら、脊髄反射で外積です。

外積で直交ベクトルを作る

2つの平行でないベクトルaとbがある時、その外積cは、aともbとも直交したベクトルになります。 両方と直交するということは、cは、aやbがいる平面に垂直に立っていることを意味します。 紙に鉛筆を立てた感じですね。

外積の計算の中身は、

c.x = (a.y * b.z) - (a.z * b.y)
c.y = (a.z * b.x) - (a.x * b.z)
c.z = (a.x * b.y) - (a.y * b.x)

となります。xを作る時はx以外、yを作る時はy以外、zを作る時はz以外です。 c.xをc0、c.yをc1、c.zをc2、というように数字をつけて 名前を変えてみると規則性がはっきりします。

c0 = (a1 * b2) - (a2 * b1)
c1 = (a2 * b0) - (a0 * b2)
c2 = (a0 * b1) - (a1 * b0)

0は12-21で、1は20-02で、2は01-10です。 Unityの場合Vector3.Cross を使えばいいので中身を書く必要はないですが、 これが身についていると便利な局面がたまにあるので、損はありません。

さて、ではどうやってpに直交するベクトルを作りましょうか?

pの他に何かもう一個ベクトルがあれば、それと外積を取ることで pに直交するベクトルが作れます。しかし、できるベクトルは平面の中にいてほしいわけですから、 用意すべきベクトルは、平面に垂直に立ったベクトルが望ましいのです。

ありますよね。確実にそうなっている奴が。a、つまり元々の回転軸です。

というわけで、aとpの外積を取りましょう。でも問題は順序です。 Cross(a,p)とCross(p,a)では向きが逆になります。 中の計算を見れば結果の符号がひっくり返ることがわかりますよね?

さて、外積でできるベクトルの方向には簡単な覚え方があります。

• +Xと+Yの外積は+Z
• +Yと+Zの外積は+X
• +Zと+Xの外積は+Y

規則性がわかりますか?xyzを012で置き換えれば、01→2、12→0、20→1となります。 そして、外積の順番を換えると方向が逆になります。

上の平面化した図が、仮にOからaが進む方向に見て書いた図だとすれば、 aは+Z軸的な感じになります。今、pが右になるようにちょっと図を回せば、X軸っぽくなりますよね。 「+Zと+Xの外積は+Y」なので、Cross(a,p)でできるqは、図中で上を向くことになります。 さっき書いた図と一緒なので、これで行きましょう。

var q = Vector3.Cross(a, p);

ここで、qとpの長さが違っていると面倒くさいので、 qの長さはpに合わせておきましょう。 そうすれば、qの終点が円周に乗って考えるのが楽になります。

q.Normalize();
q *= p.magnitude;

しかし、実はこれは不要で、qの長さはpと同じなのです。 aとbの外積は、aとbが直交していて、もしbの長さが1ならば、 結果の長さはaと同じになります。 直交していて片方の長さが1というケースでは外積が非常に便利に使えますので、 覚えておくと良いかと思います。 直交してなかったり、両方とも長さが1でなかったりすると、 大抵Normalize()が必要になります。

ベクトルを合成してV'を作る

ではpとqを使ってさらに図を描き直します。

中心Cから、V,C+q、V'までの距離は全て同じです。円周上にありますからね。 そして、角度θがわかっているので、V'がCから横にどれくらいずれているかは|p|*cosθ、 縦にどれくらいずれているかは|p|*sinθだとわかります。 横はpで、縦はqですから、

V' = C + p*cosθ + q*sinθ

と求まります。ここまでをコードにしましょう。

static Vector3 RotateVector(
    Vector3 v,
    Vector3 axisNormalized, // 軸ベクトルは要正規化
    float theta)
{
    // vを軸に射影して、回転円中心cを得る
    var c = ProjectVector(v, axisNormalized);
    var p = v - c;

    // p及びaと直交するベクタを得る
    var q = Vector3.Cross(axisNormalized, p);
    // a,pは直交していて、|a|=1なので、|q|=|p|

    // 回転後のv'の終点V'は、V' = C + s*p + t*q と表せる。
    // ここで、s=cosθ,  t=sinθ
    var s = Mathf.Cos(theta);
    var t = Mathf.Sin(theta);
    return c + (p * s) + (q * t);
}

めでたくRotateVectorが実装できました! 自分で書いた際には、テキトーなベクトルを回してテストしておきましょう。

まずは+X(1,0,0)を+Y(0,1,0)を軸にして90度回した時に+Z(0,0,1)になるか? といった簡単なテストをして粗く確かめ、大丈夫なら、 (1,2,3)あたりを(3,2,1)あたりを軸に47度みたいな汚ない角度で回してみて、 それっぽい感じになるか、角度をマイナスにしてもう一度回した時に元に戻るか、 といったあたりを確かめておくのが良いでしょう。

RotateVectorを使ってベクトルを回す

RotateVectorができたので、これを使う所に話を戻します。 ワールド座標系のbeamAxisなるベクトルを、 そのbeamAxisが+Z方向になるようなローカル座標系における角度、 φとθで回します。

あとは軸です。回す軸が定まれば、RotateVectorにφとθを渡して完了となります。 ローカル座標で回す際には、X軸に関してφ、Y軸に関してθ回せば良いのですが、 今はワールド座標におけるそれに相当する軸が必要です。

軸と言えば、直交ですね。直交と言えば?

脊髄反射で外積ですよ。

軸をでっちあげる

Transformがある場合、ローカル座標の+X方向、つまり右方向ベクトルと、 +Y方向、つまり上方向ベクトルはTransformが持っています。 しかし、今はワールド座標の+Z軸(beamAxis)しかなく、 右や上がどっちなのかはわかりません。 わからない、というよりも、決まっていないのです。

寝転がって北を向いても、立って北を向いても、+Z方向は北ですが、 寝ていれば右方向である+Xは地球の中心を向きますし、 立っていればは地平線方向を向きます。

さて、決まっていないのですから、勝手に決めましょう。 今回の用途は円錐状に散らしていて、θが360度全体なので問題になりません。

まず、beamAxisに直交したベクトルをでっちあげて、 これを右方向ベクトルとしましょう。beamAxisと何かの外積を取れば良く、 何でも良いのです。ただ、「平行ではない」 という条件はありますので、ちょっと分岐が必要になります。

Vevtor3 right;
if (Mathf.Abs(beamAxis.y) < 0.8f)
{
    right = Vector3.Cross(beamAxis, new Vector3(0f, 1f, 0f));
}
else
{
    right = Vector3.Cross(beamAxis, new Vector3(1f, 0f, 0f));
}
right.Normalize();

beamAxisのyの絶対値が0.8以下であれば、 beamAxisが(0,1,0)と平行になることはありえません。1未満ならいいんですが、 あんまり平行に近いと誤差が出るので、0.8としておきました。特に意味はありません。 この時は(0,1,0)と外積を取り、右ベクトルとします。 そして、0.8より大きい時は、代わりに(1,0,0)と外積を取ります。 いずれにしても、直交しているとは限らないので、Normalize()して長さを1にしておきます。

今回の用途では不要ですが、上ベクトルが必要なら、これも作ることができます。 ビルボード計算などでは必要になりますね。 +X方向と+Z方向があれば、こいつらの外積で+Y方向が作れます。

var up = Vector3.Cross(beamAxis, right);

+Z、+Xの順に外積を作れば+Yが出てきます。X,Zの順だと-Yが出てきますが、 今の場合どちらでもかまいません。どうせ円錐状にベクトルを生成するので、 ビーム軸でいくら回しても結果は同じだからです。 そして「両方長さ1で、直交してるものの外積」は、長さが1です。upはNormalize() しなくて良いわけです。しかし今回は右と前だけあればいいので使いません。

では、回転しましょう。

float phi, theta;
GetHemisphericalCosPoweredDistribution(out phi, out theta, n);
var v = RotateVector(beamAxis, right, phi);
v = RotateVector(v, beamAxis, theta);

長い名前のGetHemisphericalCosPoweredDistributionでφとθが出てきたら、 2回のRotateVectorを行います。 1回目は右ベクトル(+X)を軸にφ、2回目は前ベクトル(+Z)を軸にθ回します。

これで、beamAxisを円錐状に曲げたベクトルvが得られました。 サンプルでは、

v *= 1000f;
lineRenderer.SetPosition(0, cannonPos);
lineRenderer.SetPosition(1, cannonPos + v);

という具合にLineRendererに点を設定しています。 cannonPosは発射点で、今回は原点(0,0,0)です。 ビームの長さを1000にするために、vに1000を掛けておきました。

これでめでたくやりたいことができるようになりましたが、 Transformを用意した方が楽ですね!

終わりに

物体ごとにtransformがあれば不要なことをえんえん説明してきましたが、 これを自力で計算できるようなら、ゲームで使うベクトル計算は だいたいわかっていると言えます。

• 加減算
• 成分分解
• 内積による角度の求め方
• 射影
• 外積による直交ベクタの生成

という具合です。線と点の距離を求めたり、 線と面の交点を求めたり、反射させたり、といったものもありますが、 それらもそんなに難しくはありません。

応用の面から言えば「この計算をシェーダでやる」という用途があります (例えばSSAO)。 全ピクセルでランダムに散らしたベクトルをいくつも生成するという正気とは思えない手法ですが、 PLAYSTATION3時代でも気合の入った製品では使われていましたから、 お値段の高いスマホだけを相手にするなら使えるでしょう (ただSSAOに関してはベクトルを回すよりもいい手があるようです)。

また、そういう用途では、高速化の工夫が必要になるでしょう。 例えばRotateVectorは、回すベクトルと軸が直交しているとわかっていれば、 かなり計算を省略できます。前ベクトルを右ベクトルを軸にしてφ回す、 という場合、前ベクトルと右ベクトルは直交していることがわかっており、 内積は0です。内積の計算を省略でき、それを使う射影自体が不要になります。

なお、今回は紹介しませんでしたが、クォータニオン を用いて同じ計算をすることもできます。クォータニオンはたった4つのfloatの中に、 前ベクトル、右ベクトル、上ベクトルの情報を全部含むことができるので、 より汎用的に使えます。もしかしたらそっちの方が速いかもしれません。 いずれこのブログで紹介することになるでしょう。

参考文献

「ある軸であるベクトルを回転する」という計算については、 「物理のかぎしっぽ」内の「ベクトルの回転」がわかりやすいかと思います。