画面写真をクリックするとWebGLビルドに飛びます。ソースコードはgithubに置いてあります。
こんにちは。技術部平山です。
今日は先日のビーム に関連したネタです。 ビームのサンプルではビームが敵に当たると火花が散りますが、 それぞれの火花が飛ぶ方向はどう決めているのでしょうか? 今回はそれを詳しく説明します。
なお、今回は高校数学を使います。 ゲームのプログラムを書くにあたって、 「高校の数学を必要とする」というのは結構ハイレベルです。 「え?高校でハイレベル?」と思った方、幻想を持ちすぎです。 みんな受験でやったはずなのに、それを実地で役立てられる人は多くありません。 私の印象では、中学数学ですら実地で使える人は半分もおらず、 高校数学になると5人に一人もいない印象です。 私も数学は苦手で、非常に苦労して書いております。
しかし、数学ができれば、できる分野が広がります。 「数学を使うぞ!という意思がなければ絶対に書けない処理」 というものが、ゲームプログラミングにはゴロゴロしているのです。 数学を使う意思を持たない人はそういった分野に絶対に手を触れませんから、 少しでもやる意思のある人は、そういう分野で圧倒的な優位に立てます。
というわけで、この記事では、「数学をプログラミングに応用する一つの例」 をお見せしようと思います。
準備運動: 円に均一に散らす
半径1の円の上にランダムに点を散らすにはどうすればいいでしょうか? 「丸い回復ゾーンから緑のパーティクルがキラキラ出てくる」 みたいな表現をするなら欲しいですよね?
まずは数学を極力使わない手段から行きましょう。 円をすっぽり包む正方形にまず散らして、 円からはみ出したものは捨てる、というのはどうでしょうか。
float x, y; while (true) { x = Random.Range(-1f, 1f); y = Random.Range(-1f, 1f); var sqR = (x * x) + (y * y); if (sqR < 1f) { break; } }
-1から1の範囲の乱数を二つ取り、それぞれ二乗したものを足すと、 半径の二乗が出ます。二乗のままにしておくのは、平方根が遅い演算だからです。 これが1を超えていれば、半径1の円の外側の点なので、もう一度やりなおします。 この処理を抜けた所で、xとyには半径1の円に乗る点の座標が入っているわけです。
正直、円に関して言えば、これで十分実用になります。 どれくらいの率で捨てられるかを考えてみましょう。
半径1の円の面積は1*1*円周率で、円周率π(パイ)
は3.14くらいです。
これを包む正方形は一辺が2ですから、面積は2*2=4です。
円に入る確率は面積比に等しく、3.14/4ですから、75%以上は捨てずに済みます。
1000個点を生成する時に余計に生成するのは300個くらいで、
十分実用になると言えるでしょう。
このように、理論的に美しくないやり方でも、無駄が許容できるならそれで良いのです。 しかし、残念ながら「球面上に分布させる」という場合は、 こういう楽な方法がありません。そういう場合に備えて、数学を使ってやってみましょう。
とりあえず極座標にする
まず、乱数でx,yを直接決めてしまうと、どうしても円からはみ出します。 そこで、x,yを間接的に決めてみましょう。
まず、中心からの距離と、角度を乱数で決めます。
var r = Random.Range(0f, 1f); var theta = Random.Range(-Mathf.PI, Mathf.PI);
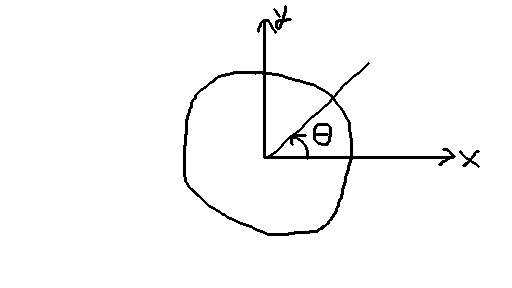
まずrに「中心からの距離」を入れます。今は半径1の円なので、 0から1の乱数です。 次にtheta(θ:シータ)に、-πからπを入れます。-180度から180度、 と度の方がわかりやすければそれでもかまいません。 ただ、次にMathf.CosやMathf.Sinを使い、その引数はラジアンでないといけませんので、 ラジアンに慣れることをお勧めしておきます。
このように、座標を「中心からの距離」と「角度」で表す座標系を 極座標 と言いまして、問題が丸い感じの時にはx,yよりも便利です。
そして、極座標のrとthetaをx,yに直します。
x = r * Mathf.Cos(theta); y = r * Mathf.Sin(theta);
三角関数は大丈夫でしょうか。

30度くらいの角度でやった時に長い方がcosで短い方がsinです。 横がcosで縦sin、と覚えてもかまいませんが、 「角度の始点が真横軸の時に」という限定がつくので注意しましょう。 テキトーに具体的な角の図を頭の中に入れておいてイメージを掴むのが大切ですね。 私は上の絵のように30度くらいの三角形を思い浮かべています。
これでとりあえず丸からはみ出さないで点を生成することができましたが、 結果はこうなります。

緑の小さなキューブを生成した座標に従って置いて、 斜め上から見た所です。妙に中心付近が明るいですよね? 分布が均一でないことを表しています。
中心にたくさんあってもかまわない用途ならこれでもいいんですが、 円の上に均一にバラまきたい、という場合にはこれではマズいのです。
均一にならない理由
では、何故均一にならないのでしょうか? それは、外側半分と内側半分に分けてみればわかります。

ひどい図ですが、内側も外側も10個づつ点を打ちました。 明らかに内側の方が密です。
rが0から0.5の内側と、rが0.5から1の外側では、 点の数は同じです。正確に言えば、点が入る確率が同じです。 しかし、面積はどうでしょう。
半径0.5の円の面積は0.5×0.5×π=0.25πで、半径1の円の面積は1×1×π=πです。 つまり、外側のドーナツの面積は(1-0.25)π=0.75πであり、 内側の円の3倍も大きいのです。 それなのに点の数が同じなのですから、当然内側の方が密になります。
つまり「内側ほど面積が小さいのに点の数が減らない」 というのが原因なのです。点の数が面積に応じて変わるように、 確率をいじらないといけません。
面積の式から比率の式に直す
半径rの円の面積は、π*r^2です(この記事では^nは「n乗」と読んでください)。
半径が1の円の面積はπですから、
半径rの円の面積と、半径1の円の面積の比は、r^2になります。
例えばrが0.5であれば、その二乗で0.25、つまり25%ですし、
rが0.7であれば、0.49、49%となります。
これは「49%の確率でrは0.7以下」ということを意味します。
この比率をpと置きましょう。
p = r^2
pは比率なので0から1です。 この式は「0から1の範囲を持つ何かとrの対応関係」を表した式であり、 先程までとは逆に、先にpを決めてしまえば、 それに対応したrが出てくることになります。 例えばp=0.25と決めれば、rは0.5になるのです。 pが0.5以下であればrはだいたい0.7以下になりますから、 pとして0から1のランダムな値をたくさん用意すれば、 そのだいたい半分はrが0.7以下に、残りの半分は0.7以上になり、 面積比に比例して点を分布させることが可能になるのです。
では、この式を使いやすくしましょう。
r=ほげほげの形にします。まず左右ひっくり返し、
r^2 = p
両辺平方根を取って、
r = sqrt(p)
rはマイナスもありえますが、今の場合は「中心からの距離」なので プラスだけでいいですね。
つまり、Random.Range(0, 1)から出てきた値のSqrtをrにすれば良さそう、 ということになります。
var r = Mathf.Sqrt(Random.Range(0f, 1f)); var theta = Random.Range(-Mathf.PI, Mathf.PI);

完璧ですね!中央に寄ってる感じがなくなりました。
一般化する
今の手続きを整理しましょう。
面積に対して均一になってほしいので、
まず面積の式を作ります。
ここで、問題にする変数が入った式を作ることが必要です。
今問題になっているのは中心からの距離rですから、
「距離がr以下になる面積」がわかる式を立てます。
先程の例で言うπ*r^2です。
そして、全体の面積に対する比率の式にします。
式の結果が0から1になるように変換するわけです。
今の場合はπを消しちゃえばそうなり、
これで変数rと比率pの関係になります。
そうして出てきた式を、今度は問題の変数に対して解きます。
A = π*r^2 // 面積の式 p = r*r // 比率の式 r = sqrt(p) // rについて解く
これでめでたく答えが出ました。 では本題に行きましょうか。
球面に散らす
球面に均一に散らします。
とりあえず、素人考えでやってできてしまえばラッキーなので、 まずは素人考えから行きましょう。
箱に散らして球面に乗る奴だけ残す
四角に散らして円に入るものだけ残す、と似た発想で簡単そうです。 コードも簡単そうですね。
while (true) { x = Random.Range(-1f, 1f); y = Random.Range(-1f, 1f); z = Random.Range(-1f, 1f); var sqR = (x * x) + (y * y) + (z * z); if (sqR == 1f) { break; } }
しかし残念ながら、これは実行しちゃダメなコードです。 テキトーに乱数を叩いて、ちょうど中心からの距離が1になる確率は ほぼゼロです。 コンピュータの場合ピッタリ1や0が出る可能性があるので、 1個だけ1か-1が出て、後の二つが0、という確率はゼロではありませんが、 1億回に1回もありません。
では、もうちょっと幅を持たせてはどうでしょうか。
while (true) { x = Random.Range(-1f, 1f); y = Random.Range(-1f, 1f); z = Random.Range(-1f, 1f); var sqR = (x * x) + (y * y) + (z * z); if ((sqR > 0.99f) && (sqR < 1.01f)) { break; } }
0.01ズレるくらいは大目に見よう、ということです。 これなら無限ループにはならないでしょうが、それほど事態は良くなりません。 確率は相当に低く、あまりにも無駄が多すぎるのです。
なお、「球の中に均一に分布」であれば、このやり方はアリです。
球の体積は4*π*r^3/3で、半径1なら4*π/3で、だいたい4くらいです。
一辺2の立方体の体積は2*2*2=8ですから、50%くらいは中に入ります。
これくらいなら許容できるでしょう。
とりあえず極座標
次は円の時と同じく、極座標にしちゃいましょう。 球は立体なので、角度が二つあります。地球儀で言えば緯度と経度です。
経度、つまり横回転の角度は360度ですね。私は0に対して対称なのが好きなので、 ここでは-180度から180度、ラジアンで言えば-πからπ、としておきます。
緯度は地球儀の場合は赤道からの角度ですね。-90度から90度、 ラジアンで言えば-0.5πから0.5πです。
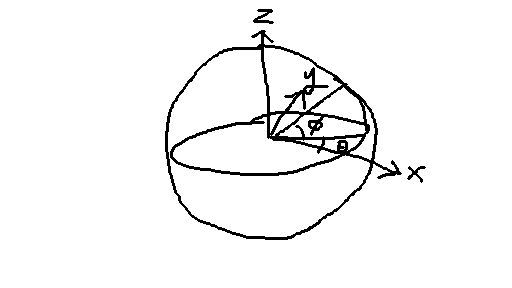
図がかなりアレですが、察してください。 経度θはx軸方向起点の横角度、緯度φ(ファイ:phi)は赤道起点の縦角度です。
南極北極をつなぐ線はZ軸としました。unityで言えば、 北極が前、南極が後ろ、といった感じです。では、コードにしてみましょう。
var theta = Random.Range(-Mathf.PI, Mathf.PI); var phi = Random.Range(-Mathf.PI * 0.5f, Mathf.PI * 0.5f);
単純に乱数で生成しただけです。 円の時と違って、中心からの距離は1固定です。球の表面ですから。 あとはこれをx,y,zに変換します。
x = Mathf.Cos(phi) * Mathf.Cos(theta); y = Mathf.Cos(phi) * Mathf.Sin(theta); z = Mathf.Sin(phi);
まず、zが最初に決まります。Z軸が上向きになるように見た時、 縦がsinφで、横がcosφです。縦がzですから、zが決まります。
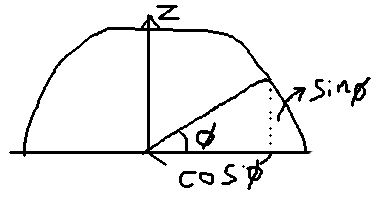
あとは、横のcosφを、xとyで分け合うわけです。
ところで余談ですが、この式、合ってるか不安になりますよね?
そんな時は、それぞれ二乗して足して1になるか確認すると安心できます。
sin^2 + cos^2 = 1を利用して変形してみましょう。
x^2 + y^2 = cos(phi)^2 * (cos(theta)^2 + sin(theta)^2) = cos(phi)^2 * 1 = cos(phi)^2
となってxとyからcosφ2が出てきます。これとzの二乗を足したら1になりますね。
さて、結果を見てみましょう。
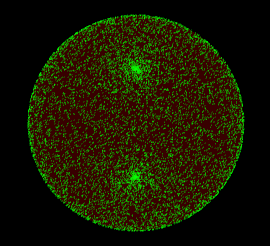
もちろんダメです。なんか2箇所に点が集まってますよね? これは北極と南極です。円の時と似たようなことが起きてしまうわけですね。 というわけで、円の時と同じ手続きでやりましょう。
まず面積を式にする
まず面積を式にする必要があります。 変数は緯度φと経度θがありますが、 問題になるのはφの方です。θは0度の場所でも、45度の場所でも、そして150度の場所でも、 範囲が2倍になれば面積も2倍になりますから、気にする必要はありません。 しかし、φは例えば同じ30度の幅でも場所によって面積が全然違います。 赤道付近の30度の面積は、極付近の30度の面積よりずっと大きいのです。

そこで、球面上の輪の面積をφで表しましょう。
が、これが円ほど簡単ではありません。「球面の、角度がφ以下の部分だけの面積」 って簡単に求まりませんよね?円とはここが違います。
まず輪の長さを表す
まず、角度φの輪の長さを式にしましょう。
先程見たように、横から見た時のcosφが横の長さで、 これが円の半径になります。

円周の長さは「直径×π」ですから、
2π*cosφですね。
積分を使う
さて、積分しましょう。 積分は長さの式を入れると面積の式が出てくる素敵な道具です(雑な説明)。
さっき作った長さの式は2π*cosφで、これを積分すると、
面積の式が出てきます(すごい雑な説明なので注意)。
証明も説明もしませんが、cosφを積分すると、sinφです。
sinの微分はcosなので、その反対ですね。
つまり、2π*sinφが球の表面積を表す式です。
実際に表面積を求めるには、φの範囲を決める必要があります。 今の場合-90度(-0.5π)から90度(0.5π)ですから、 それを式につっこみましょう。上限の値を入れた式から、下限の値を入れた式を引きます (これを定積分と言いますよね)。
2π*sin(0.5π) - 2π*sin(-0.5π) = 2π*1 - 2π*(-1) = 4π
めでたく球の表面積が得られました。4πです。
比率に直す
さて、今欲しいのは比率なので、4πで100%になるような式が欲しいわけです。
式を球全体の表面積である4πで割れば得られますね。すると0.5*sinφになります。
つまり、「緯度が-90度以上φ以下に相当する部分に点が入る確率」pは、
p = 0.5*sinφ - 0.5*sin(-0.5π) = 0.5(sinφ + 1)
となります。
変数について解く
さて、pが乱数から出てきた0から1の値に対応するわけですから、 「pが先に決まってしまった時にφを求める式」に変換しましょう。
p = 0.5(sinφ + 1)
のφが入った部分を左に、その他を右に移します。 まず2を掛けちゃいましょう。
2p = sinφ + 1
左右ひっくり返します。
sinφ + 1 = 2p
+1を移しましょう。
sinφ = 2p - 1
sinの中にφが入っていて取り出しにくいですが、
「sinの中身を取り出す関数」と言えばasinです。
アークサイン、逆正弦ですね。
sinφ = aの時、asin(a) = φというのがasinの定義なので、
φ = asin(2p - 1)
となります。めでたく求まりました。コードは、
var theta = Random.Range(-Mathf.PI, Mathf.PI); var p = Random.Range(0f, 1f); var phi = Mathf.Asin((2f * p) - 1f);
となります。結果を見てみましょう。

めでたいですね。変に集まっている場所がなくなりました。
あれ?輪郭付近に集まってない?
ところで、「輪郭付近に集まってるじゃないか」とお思いの方もいるかもしれません。 これは問題ありません。
球面上に均等に点を置いても、 横から見ると中心付近ではまばらに、輪郭付近では密に見えるわけで、 これは問題ありません。
なお、これは黒ストッキングによって脚の輪郭が強調されるのと同じ現象です。
端の方では黒い糸の密度が見掛け上高くなります。 その結果より黒く見え、脚の輪郭が強調されるのです (絶対シェーダ書いてる人いるだろ、と思ったら、やっぱりいました)。
半球
さて、球に均等に散らすことができたわけですが、 実は球面全体に散らしたいことはあまりなかったりします。
例えば、地面の上に水が吹き出す所があったとしたら、 地面にもぐる方向はいらないですよね?上半分でいいわけです。 そういうこともあって、半球の方が使用頻度は高いのです。 ビームが当たった時の火花にしても、跳ね返るのであれば 前方向はいらないですよね。ビームの進行方向逆の半球だけで良いわけです。
解く
さあ今までのやったことの応用です。
積分の範囲は-0.5πから0.5πではなく、0から0.5πになります。 下半分はいらないからです。
輪の長さの式、2π*cosφを積分して得た2π*sinφを用意し、
0から0.5πの定積分を求めます。
0.5πを入れたものから、0を入れたものを引くだけです。
2π*sin(0.5π) - 2π*sin(0) = 2π
表面積は2πです。当たり前ですよね。半分なんですから。 上の0.5πをφに置き換えた式は、
2π*sin(φ) - 2π*sin(0)
で、sin(0)は0ですから、
2π*sin(φ)
となります。次に比率にするために、表面積2πで割りましょう。
p = sin(φ)
φについて解きます。asinを使えば一瞬ですね。
φ = asin(p)
コードにすれば、
var theta = Random.Range(-Mathf.PI, Mathf.PI); var p = Random.Range(0f, 1f); var phi = Mathf.Asin(p);
です。球よりも半球の方が簡単な式になる、というのは面白いですね。

できました。半分以上あるように見えますが、 これは斜め30度上から見ているからです。
もっと極に寄せたい
さて実は、単に半球に均等に散らす、というのもイマイチ使い勝手が良くないのです。
噴水って、地面からいきなり真横に出ませんよね? もっと上の方に集中して出ます。 花火の件で言っても、ビームが当たって、真横に火花が出るのは ちょっと不自然ですよね?「跳ね返る感」を出したい場合には、 多少はビーム方向と逆向きに寄せたくなるでしょう。
そういうわけで、もっと極方向に寄せたいケースの方が多いのです。
さて、極に寄せるにもいろいろやり方があって、 例えば「φの範囲を極から30度に制限する」 というような方法は当然あります。 半球の式を作った時とほとんど同じで行けるので、簡単です。 積分の範囲を変えるだけですからね。
しかし、「角度範囲内は均一に出るが、範囲外は急に全く出なくなる」 というのは物理現象を表現する時には少々不自然です。 極が一番出やすいが、離れるほど微妙に確率が下がっていって、 赤道付近ではゼロになる、みたいな感じの方が、 使い勝手が良かったりします。
そこで、「極ほど近いほど大きな確率になるような関数を余計に掛ける」 ということを試してみましょう。
ここで掛ける関数はもちろんφの関数で、
φが0.5πの時に1、0の時に0になるような関数だと計算しやすくて都合良さそうです。
y=0.5π*φというそのまんまなものも候補になりますし、
y=sinφとsinを使うのも良さそうです。
ここでは、なだからな変化が見込めるsinを使ってみましょう。
元々輪の長さの式は2π*cosφでした。これを積分したわけですが、
積分する前に確率をいじるためのsinφを掛けます。
そして、そもそも「どうせ全部で1になるような係数で割って比率にする」
ことを考えると、前に2πみたいな定数があってもなくても結果は同じです。
面倒くさいので削ってしまって、
cosφsinφを積分することにしましょう。
さあ、もう少し高校数学を使いますよ!
積の微分法
証明しませんが、高校で習う公式に「積の微分」というものがあります。
(fg)' = fg' + f'g
こんな奴です。'がついてるのは「微分」で、f'と書けば、それは関数fの微分です。
二つの関数f,gを掛けたものを丸ごと微分すると、
それは片方だけ微分した奴を足したものになる、とこの式は言っています。
さらに、(fg' + f'g)を積分したらfgになるよ
ということも言っています。微分と積分は逆演算だからです。
なので、積分したい式をfg' + f'gと書けて、
fとgがわかっているならば、積分ができてしまう、ということになるのです
(=部分積分)。
まず、cosφやsinφは、簡単に積分できます。sinφは微分すればcosφで、
cosφは微分すれば-sinφです。これを逆に辿るだけですね。
そこで、これらをうまくfやらgにして、いい具合に元の関数を作れれば、
綺麗に積分できそうな気がしてくるわけです。
実際、f=sinφそしてg=sinφと置くと出来過ぎな結果になります。
f'=g'=cosφですから、
cosφsinφ = f'g = g'f
です。
f'g + g'f = 2cosφsinφ = (fg)'
fもgもsinφですから、
fg = sinφ^2
です。これを微分すると2cosφsinφになると。
元の式に2がくっついているので、全体を2で割れば良く、
さっき求めたfgも2で割りましょう。
結果積分した関数は0.5sinφ^2となります。
φ=0から0.5πまでの定積分は、
0.5*sin(0.5π)^2 - 0.5*sin(0) = 0.5
です。全体で0.5になるので、これが1になるように0.5で割りましょう。 つまり2を掛けます。これで比率が求まります。
p = sinφ^2
と簡単な形です。あとはφについて解きましょう。左右ひっくり返して平方根を取って、
sinφ = sqrt(p)
asinを使ってφを掘り出せば、
φ = asin(sqrt(p))
となります。コードは、
var theta = Random.Range(-Mathf.PI, Mathf.PI); var p = Random.Range(0f, 1f); var phi = Mathf.Asin(Mathf.Sqrt(p));
となりますね。

それほど中央に寄って見えませんが、 確かに端の方はまばらになっています。 sinは結構なだらかな関数なのであんまり効果が見えなかった、 ということですね。
どれくらい極に寄せるか調整したい
何か関数を掛けて確率を操作する、という方針は良さそうです。 そこでこれをもっと便利にすべく、 「どれくらい極に寄せるか」を調整できるようにしましょう。 噴水に使うならもっと中央に寄せたいですからね。
それには、sinφを何回も掛けてしまうのが簡単です。
sinφを1回掛ければ極に寄りますが、もう一度掛ければさらに極に寄ります。
例えばsinφが0.5である時、2乗すれば0.25です。
sinφが1に近い時は2乗してもほぼ1ですが、
2乗することで1に近い場所に留まるのが難しくなります。
であれば、2乗と言わず、5乗6乗としていけば、
さらに極に寄っていくはずです。0.9であっても5乗もすれば0.59まで落ちてしまいます。
掛ける回数が多ければ多いほど、より1に近い値が乱数で出ないと極から離れていられない、
ということになります。
というわけで、掛ける関数をsinφ^nにしてみましょう。
nは調整可能なパラメータということになります。
ただし、問題はこれが積分できるかどうかです。
積分
ではcosφsinφ^nを積分しましょう。
「積の微分」の公式が今回も使えそうですが、さっきみたいに
fg両方をsinφにするような楽なマネはできそうもありません。
sinφ^nは積分が面倒くさそうなので、とりあえずこれをgとし、
cosφはf'としましょうか。
f' = cosφ f = sinφ g = sinφ^n g' = ?
sinφ^nの微分はどうしたらいいでしょうか?
ここで、微分の公式にはもう一個有名な奴があります。
df(u(x))/dx = df/du * du/dx
今、xの関数u(x)というのがあって、 さらにuを変数とするf(u)という関数があった時に、 fをxで微分した時の結果は、fをuで微分したものと、uをxで微分したものを 掛けたものだ、という公式です。
微分という奴は「何で微分するか」というのが大事です。
f'みたいに'をつけてもいいのは、変数が一個しかない時だけで、
今のようにuとxで二つ変数がある場合、
「fをuで微分した」のように「何で」が必要になります。
df/duみたいに面倒な記法が必要なのはそれが理由です。
さて、この公式が何がおいしいか?
「なんかややこしい式の時に、テキトーな部分を丸ごと変数とみなしてしまえる」
ことです。今sinφ^nを微分したいわけですが、
sinφが邪魔くさいわけです。これをテキトーにuとでも置けば、
u^nになり、式が簡単になります。
これは多項式の微分であり、
(x^n)' = n*x^(n-1)
です。何乗してるかを表すn前に出てきて、「何乗」のnが1下がります。
x^3は3x^2になりますよね。というわけなので、
sinφ^nは、u=sinφと置いてしまえば、uで簡単に微分できます。
d(u^n)/du = n*u^(n-1)
ここで、uがxで微分できれば、それを掛ければ答えになる、 とさっきの公式は言っているのです。
du/dx = d(sinφ)/dx = cosφ
sinφの微分はcosφですね。なので全部つなげると、
df(sinφ^n)/dφ = d(u^n)/du * d(sinφ)/dφ = n*u^(n-1) * cosφ = n*cosφ*sinφ^(n-1)
となります。微分してずいぶん汚くなりましたね。大丈夫でしょうか。
f' = cosφ f = sinφ g = sinφ^n g' = n*cosφ*sinφ^(n-1)
とりあえず、つっこんでみましょう。
(fg)' = f'g + fg' = cosφ*sinφ^n + sinφ*(n*cosφ*sinφ^(n-1)) = (1+n)cosφ*sinφ^n
cosφ*sinφ^nがうまいこと出てきたので、どうにか整理できました。
さて、元々積分したかったのはcosφsinφ^nなので、(1+n)が余計です。
割っちゃいましょう。
(fg)'/(1+n) = (f'g + fg')/(1+n) = cosφsinφ^n
ということなので、欲しい積分後の関数は、fとgを掛けて(1+n)で割った、
sinφ^(n+1) / (n+1)
となります。さて、さっきまではこの状態で全体の積分値を求めてましたが、 どうせ比率にしちゃうので、前についてる定数を先に捨ててしまってもいいはずです。
sinφ^(n+1)
簡単になりました。 0から0.5πまでの定積分を求めると、
sin(0)^(n+1) - sin(0.5π)^(n+1) = 0 - (-1) = 1
となり、丁度1です。何も割らずに済みますね。つまり、 比率pに関する式は、
p = sinφ^(n+1)
です。解きましょう。左右ひっくり返してから、両辺n+1乗根を取ります。 「k乗根を取る」というのは「1/k乗する」ということなので、 powを使いましょうか。
cosφ = pow(p, 1/(n+1))
さらにasinを使ってφを掘り出します。
φ = asin(pow(p, 1/(n+1))
コードにしましょう。
var theta = Random.Range(-Mathf.PI, Mathf.PI); var p = Random.Range(0f, 1f); var phi = Mathf.Asin(Mathf.Pow(p, 1f / (n + 1f)));
サンプルではnを調整するスライダーをつけてあります。

2,4,8...と増えるほど極に寄っていきますね。
なお、n=0の時の式は、「半球で均一に分布」と同じになります。 0乗は1なので、Asinの中はただのpになりますね。 さらにn=1の時には最初にsinφを掛けた時と同じ式になります。 pの0.5乗、というのはsqrtのことです。 かくして、この関数を用意しておけば、 いろんな散り方を実現できるわけです。
余談: nの調整
nに128という大きな値を入れても、一点に集まってしまうほどにはなりません。 それこそ数千とか数万を入れる必要があります。 nが大きくなるほど、1大きくすることの影響が小さくなっていくのです。
こういう時には対数ですね。 デシベルの時と同じです。 サンプルでは実際、対数化したスライダーを置いています。
ちなみに、今回のcosφsinφ^nという式は反射光を描画する時によく使われた式でして、
nは、大きな値を入れるほど「ツルッとした質感」、小さいほど「ザラっとした質感」
になるパラメータとして使われていました。
実は、照明計算の分布関数を、火花を散らすのに応用したのです。
終わりに
このように、ゲーム作りにおいては、高校数学が役に立つ局面があります。 ベクトルはとりわけ重要で、次に三角関数、そして行列、微積分と続きます。
今回の内容は全て高校の教科書の範囲でして、 本来はみんなできているはずのことです。 しかしいざ仕事で必要な状況に出会っても、なかなか応用ができません。 それどころか、「微積使えば解ける奴だ」ということに気づくことすら 難しいのが現実です。ググってそのものズバリが出てこなければお手あげ、 という状況になってしまうのは、「数学で解けるんじゃないか?」 という発想がそもそも出てこないからでしょう。
数学にイマイチ苦手感がある人には、 中学数学からやるのが良いかもしれません。 「東大の先生! 文系の私に超わかりやすく数学を教えてください!」 という本が素晴らしすぎるので、おすすめしておきます。
手順まとめ
では、今回の手順をまとめておきましょう。
- 長さを表す式を立てる
- 確率を操作したければ何かテキトーに関数を掛ける
- 積分する
- 端から端まで積分した時の値で式を割って比率にする(=累積分布関数を作る)
- 逆関数を求める
となります。
均等分布ならば積分すると面積になりますが、確率をいじって、
比率に直してしまった後はもはや面積ではなく、
累積分布関数
と呼びます。
記事でp=ほげほげと書いてきた式ですね。
「変数の始点からある値までの間に入る確率」のことです。
この累積分布関数の逆関数を求めて元の変数について解けば、 0から1の乱数を入力するといい感じの変数が出てくる式、ができるわけです。
補足: 他で見たのと式/コードが違う
他の文献ではsinとcosが入れ替わっているものをよく見かけると思います。 実際、ビームのサンプルにも同じ関数がありますが、sinとcos、 asinとacosが入れ替わっています。 これは、ビームのサンプルではφが極起点で、 今回は赤道起点だからです。φの定義が異なっています。
一般的な極座標では極起点で、大抵はその方が便利です。 しかし今回は「緯度」という言葉を使う方が理解しやすいだろうと考え、 赤道起点で書いています。 極起点で角度を測りたい時は、自分で導出をやりなおしてみてくださいね!
次回予告
次回はこうやって求めた「散らした点」をどう実際に使うか、 という所をご説明します。 このままだと「半径1の半球に散らした点」でしかなく、これだけでは用途が限られます。 任意の方向に動くビームを曲げるとか、任意のベクトルの周囲に粒子を飛ばす、 とかいう用途に使うにはもう一工夫必要なのです。
