画面写真をクリックするとサンプルのWebGLビルドに飛びます。
こんにちは。技術部平山です。
今回は、トラックボール 状のものを操作してカメラを動かす機能を作ってみました。 上のサンプルを触ってみてください。 右上の球をトラックボールだと思って回してみれば、 だいたいそんな感じにカメラが動きます。 また、ドラッグしながらマウスボタンを離す(タッチなら指を離す)と、 慣性でグルグル周ります。
実用性には疑問がありますが、 これはクォータニオンを無理矢理応用してみた結果です。 せっかくなので紹介いたします。
動機
クォータニオンはUnityの基幹的な部分でも使われていますが、 直接触ることはあまりありません。 しかし、クォータニオンがあると楽にやれることや、 クォータニオンでないとできないこともあります。
そういうわけで、クォータニオンを布教したくてたまらないのですが、 そもそも私がクォータニオンをよくわかってない という重大な問題があります。 そこで、数学はともかくとして、 「クォータニオンを使ったらこういうのが作れた」という例を出して、 誰かが興味を持ってくれるのを待とう、と思ったわけです。
さて、問題は何にクォータニオンを使うかです。
最近たまたま計算でメッシュを作ることがありまして、 それをいろんな角度から見たくなりました。 Sceneビューなら自由にカメラを回せるのですが、 Gameビューで見たいこともありますし、 ビルドで見たいこともあります。 デバグ用のカメラを実機で使えるようにすることも多いですよね。 今回はそれにクォータニオンを使ってみることにしました。
今回のソースコードは別の用途で作ったサンプル の中にあります。BallCameraController.csがそれです。
回転をTransformに反映させる所
まず、現在の回転状態をクォータニオンで保持します。 クォータニオンは回転行列やオイラー角と同じく、 3軸の回転状態を保持できるデータです。 東西南北のどの方角を向いて、 上下にどれくらい首を動かして、 左右にどれくらい傾いているか、 という3軸ですね。 よくこの「3軸の回転状態」のことを「姿勢」と 呼んだりします。短いのでこの記事でもこの言葉を使いましょう。
このクォータニオンに、画面右上のボールの操作を反映させて、 姿勢を回していきます。ここの詳細は後にしましょう。
そして、毎フレーム姿勢からカメラ位置と、 カメラの向きを生成し、 カメラのTransformにセットします。
カメラの位置は、 (0,0,-1)をクォータニオンで回して、指定の距離(サンプルでは3) を掛けたベクトルを、 設定した中心座標(サンプルでは(0,0,0))に 加えることで得られます。
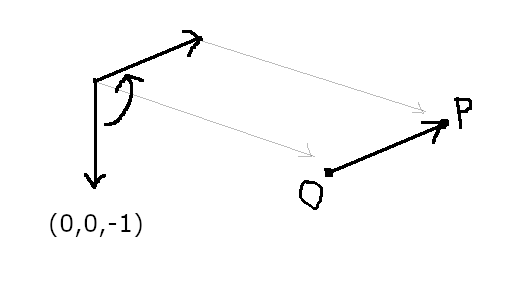
なお、(0,0,-1)である必要はありません。 クォータニオンの回転の基準方向をどこに取るかは自由です。 しかしUnityに合わせないと不便なので、 ここではUnityに合わせて(0,0,-1)にしてあります。 クォータニオンがデフォルト値の時に、カメラが+Z方向を向く、 という設定です。
コードはこんな感じです。
var v = orientation * new Vector3(0f, 0f, -1f); attachedCamera.transform.position = o + (v * distance); attachedCamera.transform.rotation = orientation;
orientationはクォータニオンで、
これに(0,0,-1)を「作用させる」と、回ったvが出てきます。
「作用させる」の詳細は今回は触れませんが、
Vector3 v = orientation * new Vector3(0f, 0f, -1f);
というようにQuaternionクラスの乗算演算子でやれます。 一見掛け算に見えますが、クォータニオンの掛け算は別にあり、 これは掛け算ではないことに注意が必要です。
さて、このvに、指定した距離distanceを掛けて、 カメラが動く際の中心座標であるoを足せば、 カメラの位置が出来ます。
そして、カメラのTransform.rotationには
orientationをそのままつっこみます。
これで、クォータニオンが
カメラに反映されるようになりました。
次はクォータニオンそのものをどう計算するかを見ましょう。
角速度を積分する
毎フレーム小さな回転を作って、 その回転でクォータニオンの値を微妙に変えて行くわけですが、 これはつまり積分です。 ここでは理屈はすっ飛ばして、結果だけ使いましょう。
orientation += orientation * (angularVelocity * (0.5 * dt))
一番簡単な、オイラー法による積分です。 数学めいた記法を使わずコードっぽく書きましたが、 これはUnityでは動きません。
- Quaternionクラスに+演算子がない
- Quaternion * Vector3は先程の「作用させる」になり、「掛け算」にならない。
といった理由によります。
さて、dtは要するにTime.deltaTimeで、
フレームレートが高いほど小さくなって、より細かな単位で更新します。
angularVelocityは角速度で、オイラー角と同様Vector3です。
「1秒あたりのxyz角度変化」を意味します。
つまりこの式は、
Time.deltaTimeの半分を角速度に掛けて、
現在の姿勢を表すクォータニオンで回し、
できたものを、現在のクォータニオンに足す、
ということを意味しています。
では、実際に動くコードにしてみましょう。
static Quaternion UpdateOrientation(Quaternion q, Vector3 w, float dt) { var t = w * (0.5f * dt); var dq = q * new Quaternion(t.x, t.y, t.z, 0f); q = new Quaternion( q.x + dq.x, q.y + dq.y, q.z + dq.z, q.w + dq.w); q.Normalize(); return q; }
qが姿勢(先程までのorientation)で、wが角速度(先程までのangularVelocity)です。
1行目で、角速度に0.5*dtを掛けてtに入れています。
そして、ここからQuaternionのコンストラクタを使ってクォータニオンに変換し、
クォータニオン同士の乗算を行います。これで先程の式の右辺ができました。
最後に、加算演算子がないので、コンストラクタに要素ごとに加算したものを渡して
加算します。ちょっと面倒ですが方法がみつかりませんでした。
なお、最後のNormalize()は、加算によって大きさが狂うのを補正するためのもので、 ないとだんだん大きさが狂ってきます。
さて、これで、角速度があればクォータニオンを更新できる、 という状態になりました。角速度を作りましょう。
入力から角速度を作る
今回はトラックボール を模しています。なので、
- ボールを前後に回すと、カメラが上下に動く。回転軸はビュー空間のX軸。
- ボールを左右に回すと、カメラが左右に動く。回転軸はビュー空間のY軸。
- ボールの側面をこする、あるいは指でつまんで独楽のように回すと、視界が傾いて天地がひっくり返る。回転軸はビュー空間のZ軸。
といった感じになってほしいわけです。
画面上にあるボールのどこをタップして、どうドラッグするかで、 この3種類の回転をブレンドすればいいのですが、少々の数学を使います。
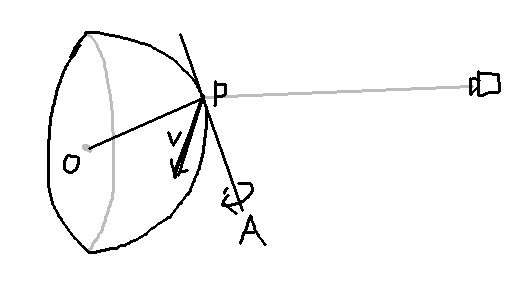
カメラから見えるのは手前の半球だけなので、図には半分だけ球を書きました。 カメラが右側にある感じです。
まず、視点から出たレイが入力用の球に当たる点Pを求めます。 球の中心をOとしましょう。 さらに、ドラッグ方向ベクトルをVとします(手前を向いているつもりで図を描きました)。 PをつかんでV方向に引っ張る回転は、 図中のAを軸とした回転です。 AはVともOPとも直交しているので、 OPとVの外積で作れます。
角速度(x,y,z)は、ベクトル(x,y,z)を 軸とした回転を意味し、 ベクトルが大きいほど回転が速いことになるので、 今計算したAは角速度そのものとして使えます。 Vが大きいほど、つまりドラッグが速いほど、 Aも長くなりますから、回転は速くなります。
というわけで、やることは、
- レイが球と当たる場所Pを求める
- 球の中心OからPへのベクトルを用意する
- ドラッグベクトルVを用意する
- 外積で軸を求める
- 軸をカメラのビュー座標系に移して角速度とする
となります。なお最終的な角速度は、 回転するもののローカル座標での値が必要です。 今はカメラが回るので、 「カメラのローカル座標」といえばビュー座標系です。
ところで、サンプルでは触り心地を良くするために計算をスクリーン座標系で行っており、 そのために少し計算が複雑になっています。 しかし、ワールド座標系で行って、できた軸をビュー座標系に移す方が簡単です。
入力用の球をSphereCollider として用意した場合、 OnBeginDrag に渡ってくるPointerEventDataから、
var p = data.pointerCurrentRaycast.worldPosition
であっさりワールド座標系の点Pが取れます。
慣性について
このサンプルでは、勢いよくボールを回すように入力すると、 慣性でしばらくカメラが回り続けます。 上のgif動画にも出てきますね。
これは単に角速度を毎フレーム減衰させているだけです。
angularVelocity *= (1f - (dt * Drag));
しかし、この慣性を表現するには、回転を積分できる必要があります。 これがクォータニオン以外ではなかなかうまくできません。 オイラー角だと綺麗に回りませんし (ホーミングの時にも述べましたね)、 行列でやると上の積分計算が結構面倒くさくなります。 クォータニオンだとこれが恐ろしく楽なのです。
クォータニオンの用途について整理
私が知る範囲での話ですが、クォータニオンが使える用途はだいたい 以下のような感じです。
- ある回転を他のものにも適用する。
- 物をある向きからある向きへゆっくり回す、あるいは補間をする。
- 積分する。
- 回転に使うデータ量を減らす
「回転を他のものにも適用する」というのは、 例えば、東を向いている人が、南を向きながら上を向くような 回転をしたとして、これと同じ回転を、西を向いた人にも行う、というような話です。 これには行列やクォータニオンが必要で、 オイラー角だけではそれができません。
そして、物をゆっくり回す場合は、 間の状態を作れないといけないので、補間が必要になります。 これはクォータニオンの独壇場です。 球面線形補間が有名ですね。 積分ができるのも、これと似た長所です。 未来の結果がわかっているのが補間で、わかっていないのが積分、 というだけで、「アニメーションする」ということでは同じです。
そして最後の「データ量を減らす」ですが、 クォータニオンはfloat4つで済み、行列のfloat9個より小さくて済みます。 シェーダに送る、というような時にはそれがおいしい時もあるでしょう。
なお、私が思うクォータニオンの利点として、 「角度を経由しないで済む」ということがあります。 角度をベクトルにするには、三角関数が必要です。 面倒で重い上に、ベクトルから角度に戻す際には激しく精度が落ちます。 角度は中学数学までの範囲でも理解できるので 安心感はありますが、ベクトル演算が使えるのであれば、 角度はできるだけ通らない方が楽な気がします。
クォータニオンはベクトルとの親和性が良く、 大抵のことは角度を経由せずにやれます。 クォータニオンを使っていてsin/cosが出てきたら、 無駄な遠回りをしているかもしれません。
参考文献
さて、どうでしょう。 クォータニオンが気になってきましたか? そういった方には、 もっとちゃんとした説明をおすすめしておきます。
私の数学力ではこれらのサイトのちゃんとした理解はまだ難しいのですが、 逆に言えば、それでも便利と感じるくらいには使える、ということでもあります。
- クォータニオン (Quaternion) を総整理! ~ 三次元物体の回転と姿勢を鮮やかに扱う ~
- Unityを例にしているので我々には読みやすいですし、相当理解が深い人が書いているんだろうなという迫力があります。
- クォータニオン計算便利ノート
- 実地で使うための知識が短くまとまっていてとても助かります。
- ベクトル・複素数・クォータニオン
- たぶん数学的にも最強の説明だと思うのですが、私にはまだ早いようです。最初に読んだのは17年も前ですが...
終わりに
「わからなくても使えて便利だよ!」的なノリで書いてきておいて何ですが、 「使うためにあった方がいい知識」 というものは当然のようにあります。 クォータニオンは勉強しないで使うには危険すぎる道具です。
例えば私は角速度をワールド座標系で用意して バグっていましたが、 それは根本的な理解があれば絶対やらかさないようなバグです。
積分の式は、 「ローカル座標系の角速度に、クォータニオンを作用させてワールド座標系の小さな回転を作り、それを加算している」 という意味があるのですが、それがわかっていないからこそ 角速度をワールド座標系で用意するようなバグをやらかすのです。
というわけなので、これからもより深い理解を得るべく勉強したいところですが、 それはそれとして、 「理解してから使おう」なんて言っていると使えなくなってしまうので、 「とにかく使ってみる」も大事かなと思います。 今回はその一例です。