
こんにちは!カヤック面白プロデュース事業部のおばらです。
普段は受託案件、特にインタラクティブな WebGL や Canvas2D を駆使する案件のデザイン&実装を担当しています。
先日出題したJS体操 第1問目、挑戦してくださったみなさまありがとうございました!
早速ですが最短文字数の回答は 44文字 でした!
export default x=>x-(x%=.2)+.2-(.04-x*x)**.5
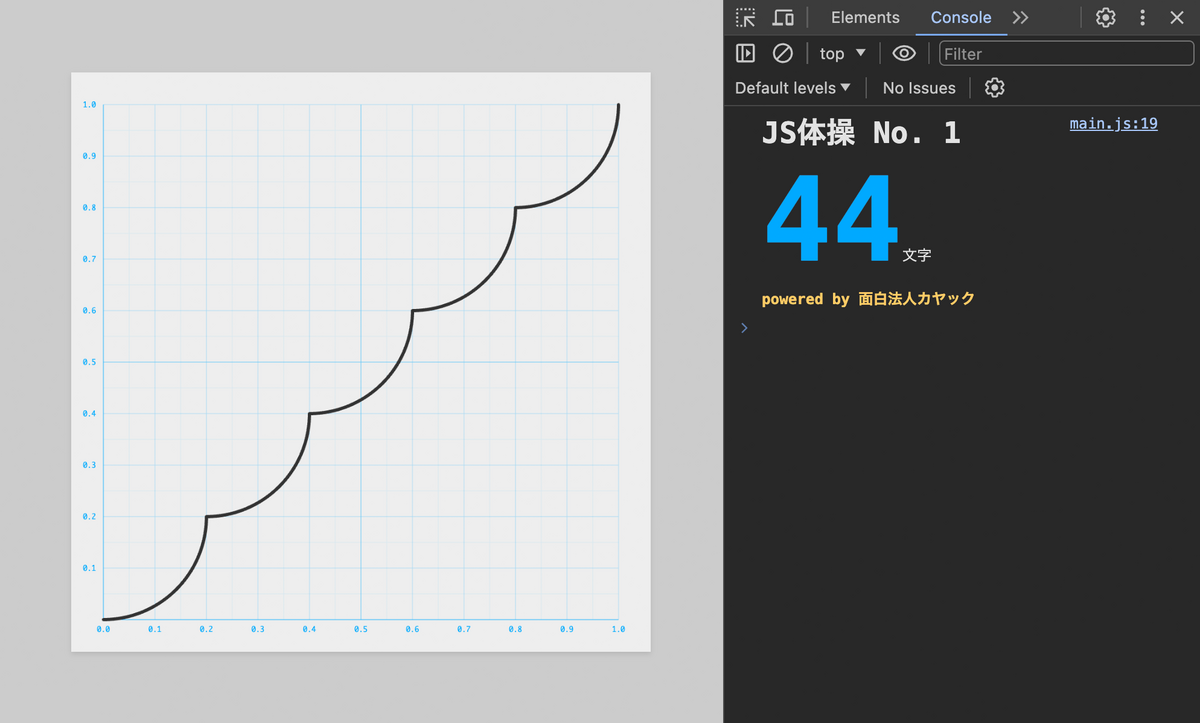
みごと44文字を達成した方は、
- halwhite さん
- koyama41 さん
- sugyan さん
- tkihira さん
- たつけん さん
の5名!(※ Unicode コードポイント順)
おめでとうございます!!
最短文字数を狙った正統派の回答以外にも、裏技的な面白アプローチがたくさんありました笑
このアプローチは面白い、ぜひ紹介したい!という回答がいくつかあったので、解説記事は2回に分けてお送りしようと思います。
- 第1回(本記事)最短文字数44文字の解説、実務での応用例の紹介
- 第2回(次回)その他の面白いアプローチの回答、裏技的な回答の紹介
なお、締切は一応過ぎましたがまだ回答の送信は(いつでも)可能です。 締切は過ぎたけど「44文字よりも短くできた!」という方はぜひ送信お願いします。
もし「まだ挑戦していない!」という方はこの記事をそっと閉じ、ぜひ『JS体操』してみてください!
『JS体操』とは?

『JS体操』とはカヤックが主催する JavaScript のコードゴルフ大会です。
今回がその第1回目でしたが、もともとは社内の勉強会として始めた施策です。
その詳細は以下のブログ記事を御覧ください!
問題のおさらい
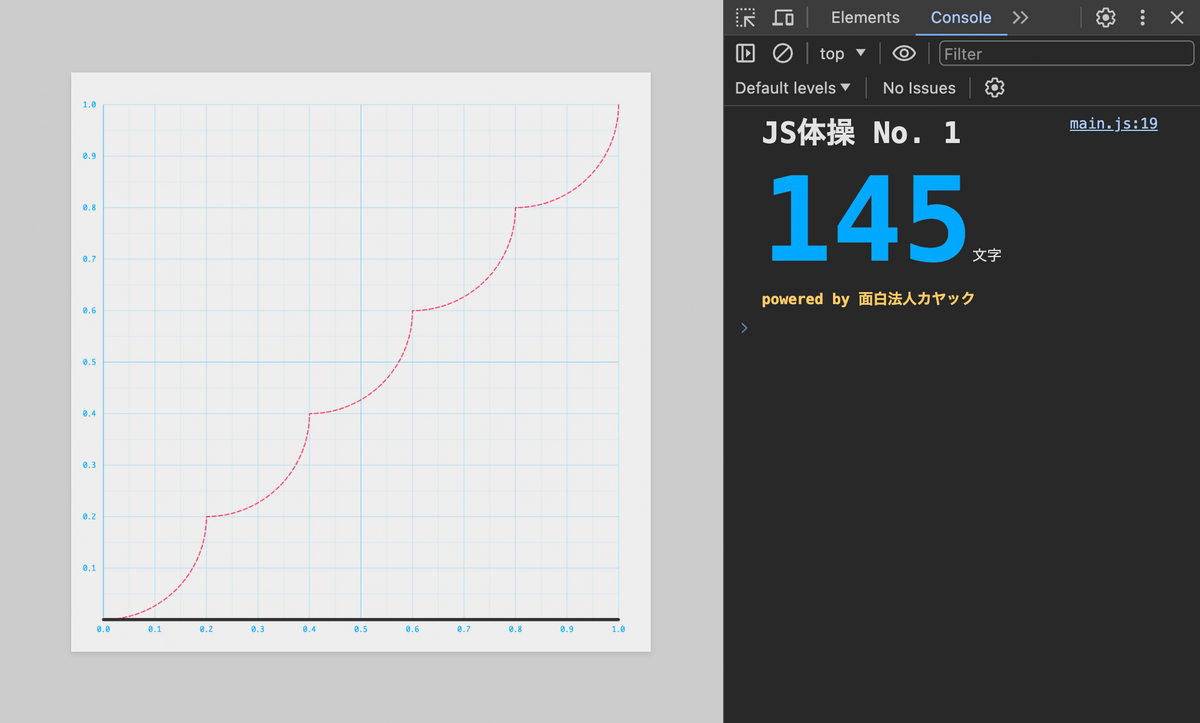
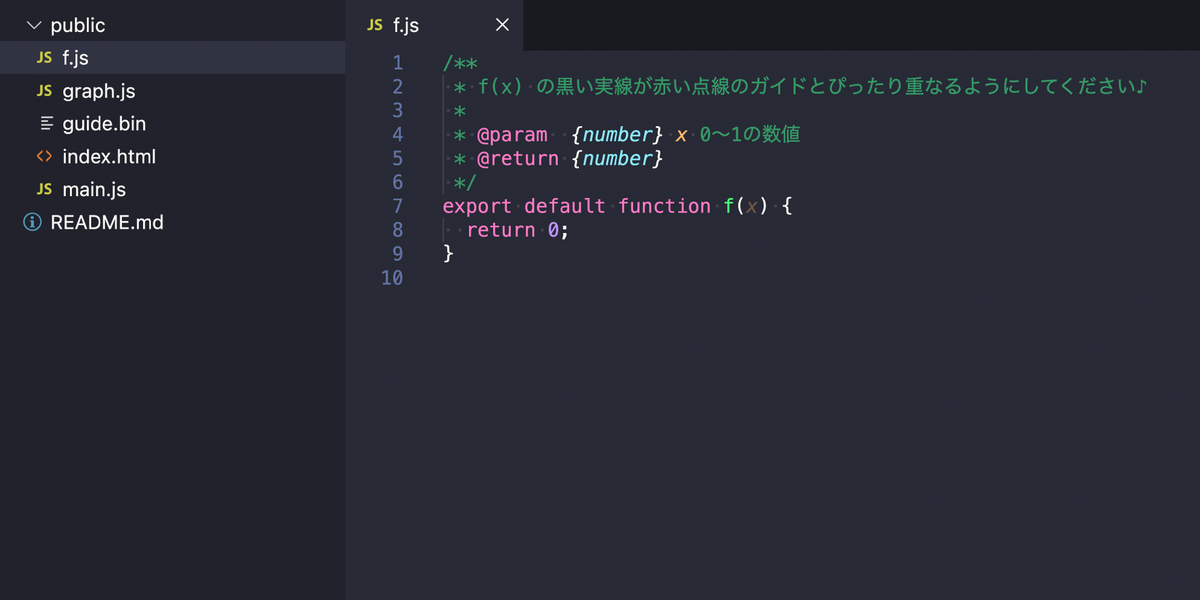
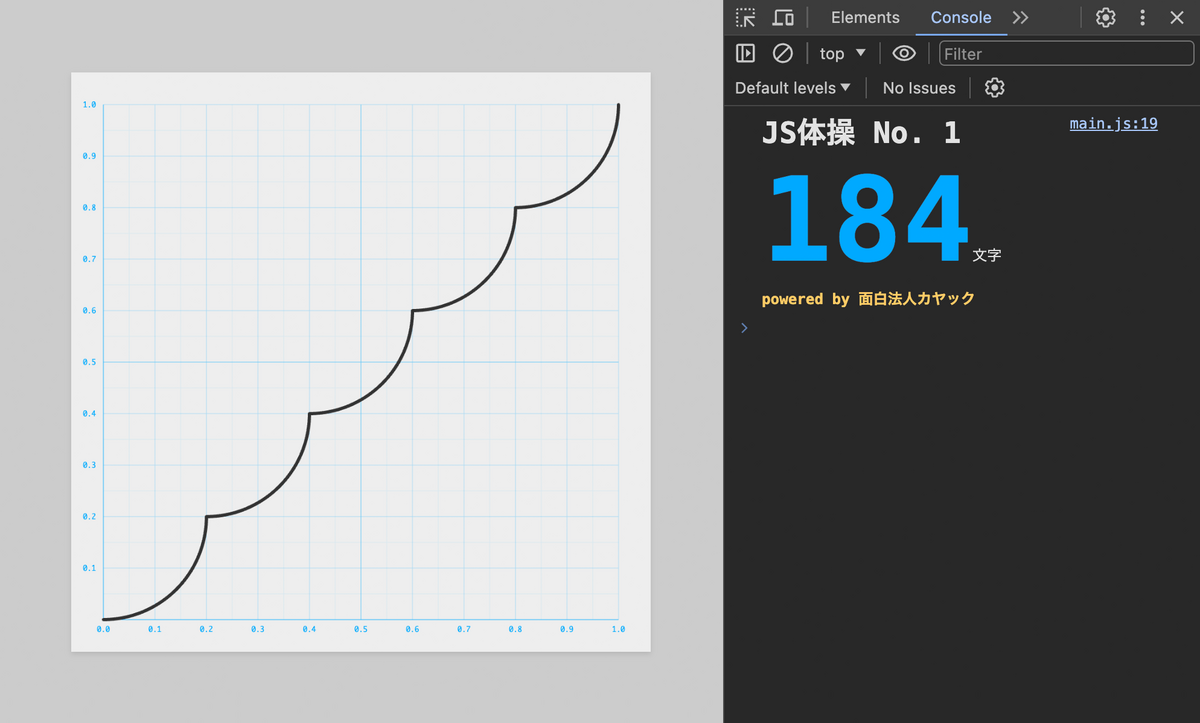
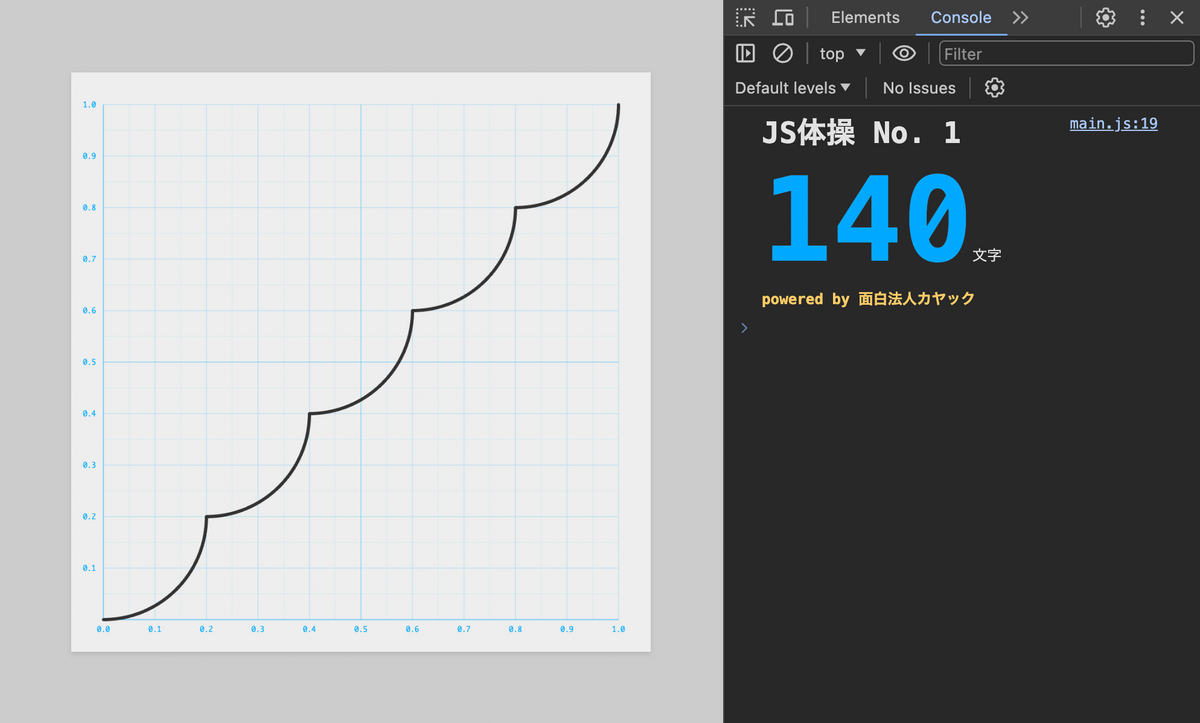
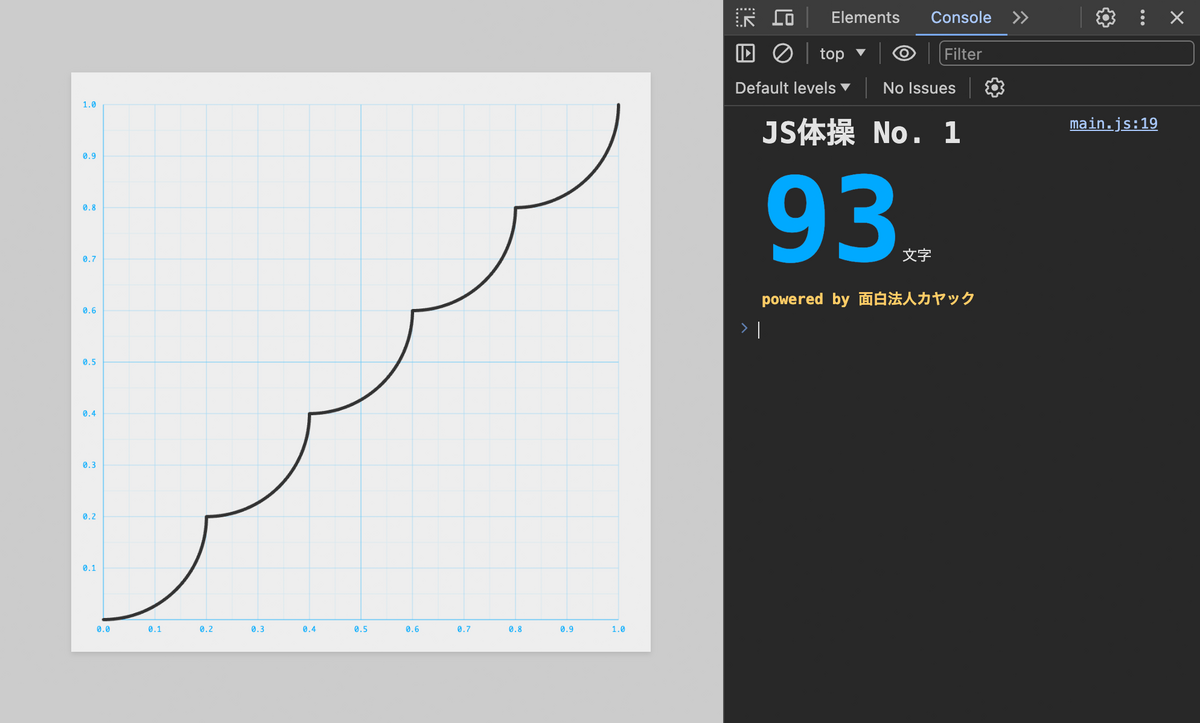
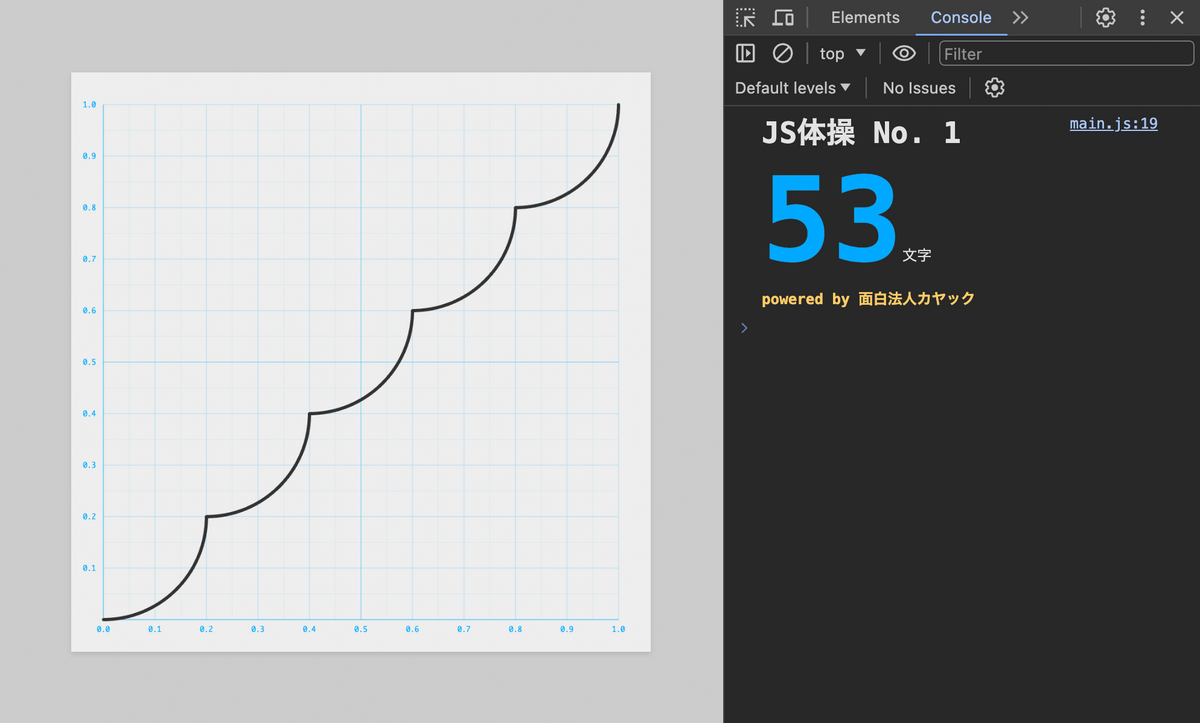
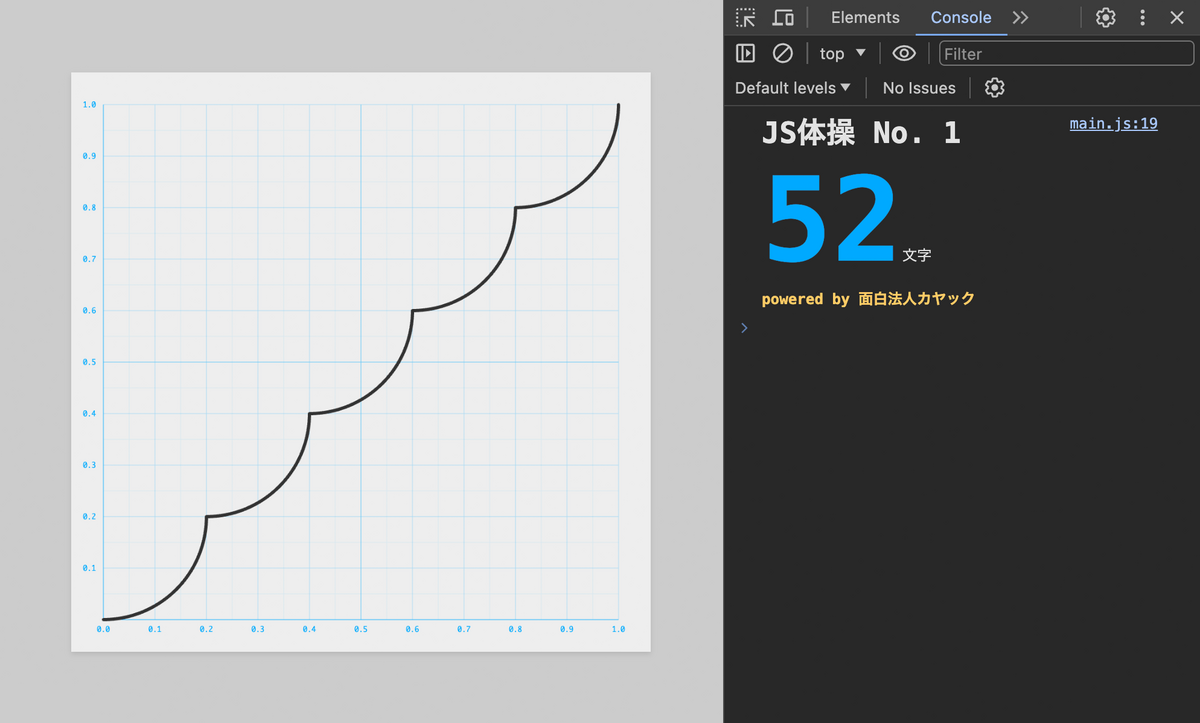
黒い実線が赤い点線のガイドとぴったり重なるように f.js を編集し、且つコードの文字数をできるだけ短くしてください!
波形を整形する問題ですね!
波形の整形はアニメーションに使うイージング関数を自作 or カスタマイズしたりする際に必要なテクニックです。
画像処理でトーンカーブをいじりたいときなどに使うケースもあるでしょう。
それにしても変な形のグラフです。
どんな式(コード)になるのでしょうか?
考えていきましょう!
考え方
複雑な形状のグラフを、複数のシンプルなグラフを合成したもの、と考えてみましょう。
グラフを図形的に捉えると、以下のように2つの図形の「足し算」や「引き算」で表せそうです。
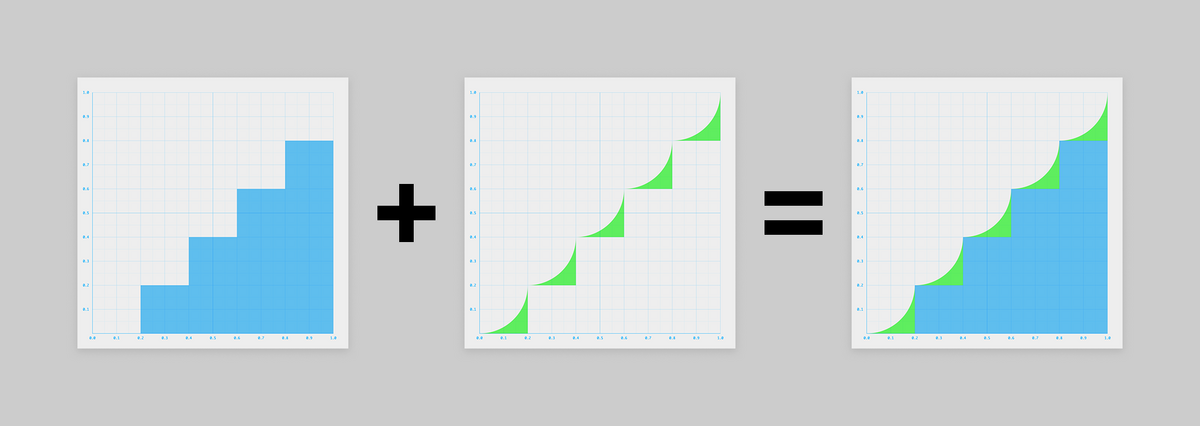
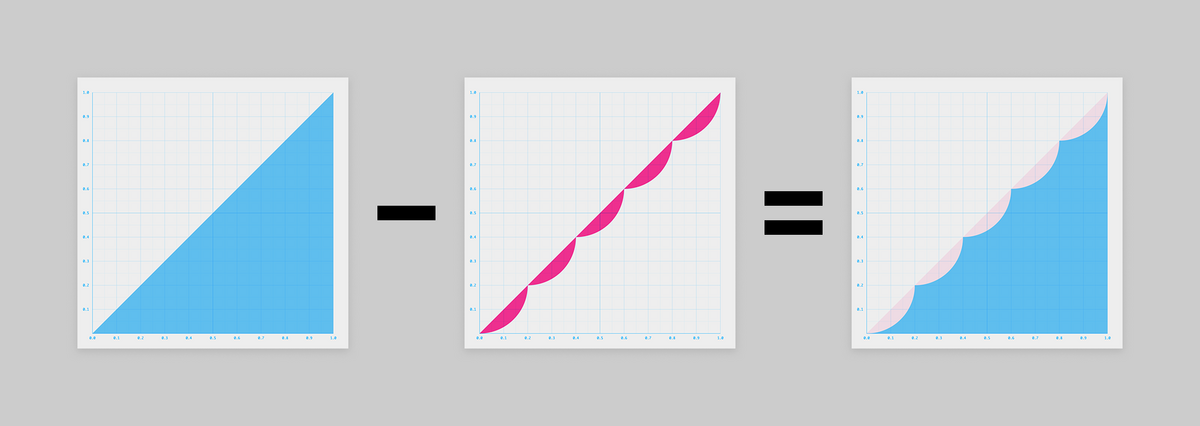
足したり引いたりしているグラフは比較的シンプルなので、ちょっと考えやすくなりましたね!
というわけで「足し算」作戦と「引き算」作戦のそれぞれを試してみましょう。
さぁ、Let's JS体操!
作戦① 足し算

上の図を数学的に考え、2つのグラフ(関数)の和と捉え直してみると、こうです!
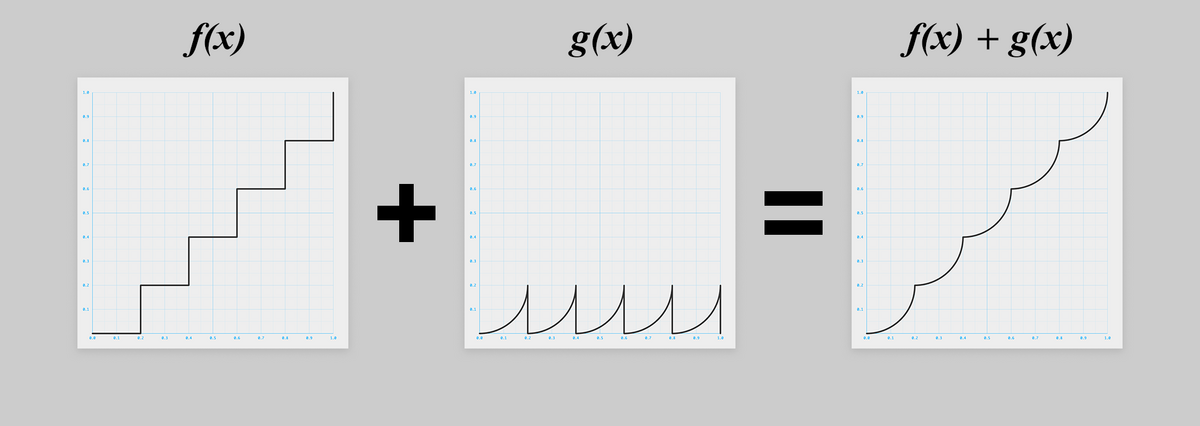
と
の2つの式が求まれば良さそうです。
f(x) を考える

は床関数(floor function)と呼ばれるグラフ(関数)です。
を JavaScript で書くと、例えばこうです。
const f = x => { return Math.floor(5 * x) / 5; };
数学的には以下も同じです。しかし後述の理由により JavaScript 的には同じとは言い切れません。
const f = x => { return Math.floor(x / 0.2) * 0.2; };
今回はコードゴルフする前提なのでより文字数が短い前者でいきましょう。
つまりこちら。
const f = x => { return Math.floor(5 * x) / 5; };
さらに今のうちになるべく短くしておきましょう。
まず return を省略します。
const f = x => Math.floor(5 * x) / 5;
Math.floor(n) は であれば
Math.trunc(n) で代替できますね。
そして Math.trunc(n)は(整数部分に)副作用の無いビット演算で代替できます。
副作用がなければどんなビット演算でもよいです。
例えば n >>> 0、n >> 0、n << 0、~~n、n | 0 など。
今回は一番文字数の少ない n | 0 を使いましょう。
const f = x => (5 * x | 0) / 5;
※ ビット演算により数値の内部的な型が64ビットの浮動小数点から符号付き32ビット整数となり、その結果小数部分が切り捨てられます
※ ビット演算の副作用を利用する際、値が符号付き32ビット整数で表現できる範囲を超えてオーバーフローしないように注意しましょう
※ 演算子の優先順位に注意しましょう

無事、床関数が描けました!
g(x) を考える
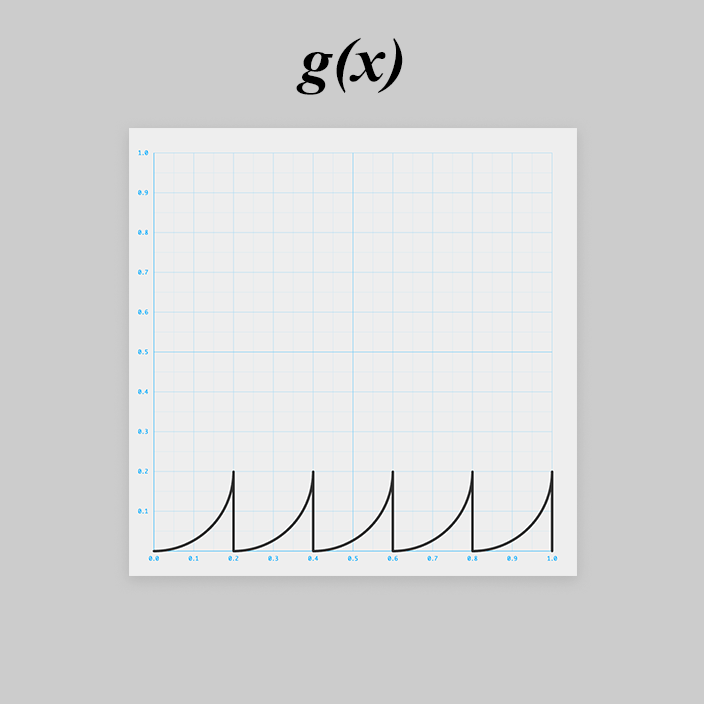
はちょっと厄介そうですね。
同じ形状が5つ並ぶ周期的な関数です。
まずはその1つを と置きます。
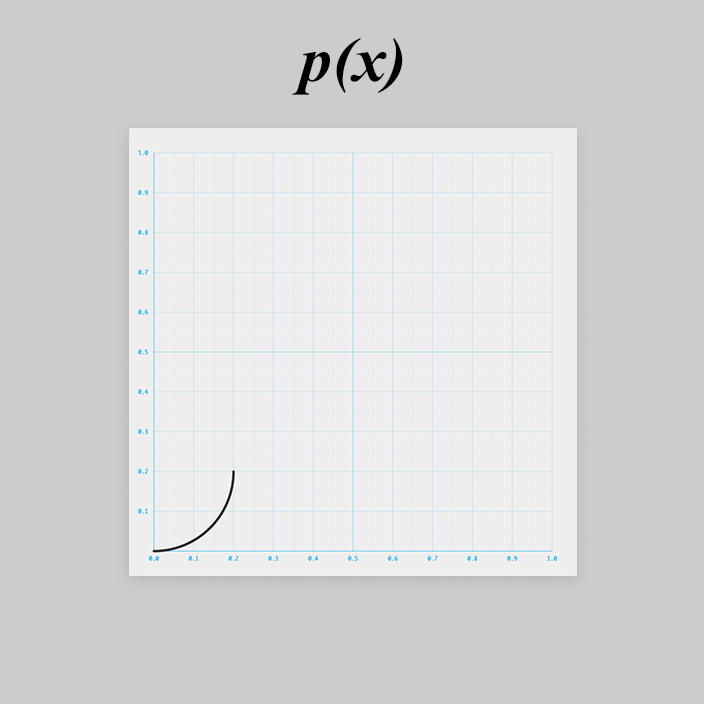
このカーブは、ぱっとみ、円の右下1/4っぽいです。
円の式から作っていきましょう。
※ 以降、数学的に厳密には正しくない説明があるかもしれませんがご容赦ください
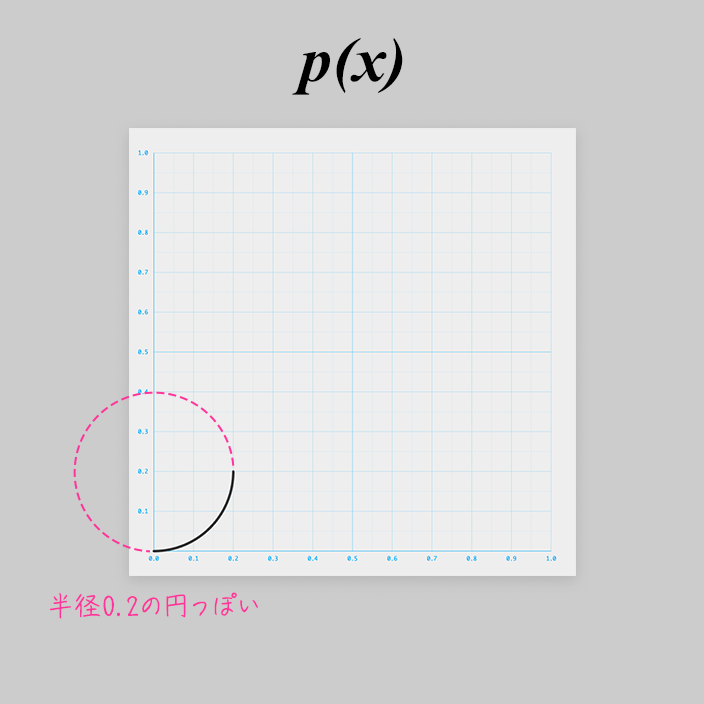
原点を中心とする半径 0.2 の円の式は以下です。
軸の正の方向に 0.2 ずらします。
最終的に の形にしたいため、
を右辺に移動します。
次に2乗を外します。
今回必要な範囲では より
最後に を右辺に移動して
できた!


JavaScript で書き直すと、
const p = x => { return 0.2 - Math.sqrt( Math.pow(0.2, 2) - Math.pow(x, 2) ); };
は
の
乗なので
Math.sqrt(n) は Math.pow(n, 0.5) と書き直せますね。
そして Math.pow(n, m) は ES2016 から使えるべき乗演算子(exponentiation operator)を用いて n**m と書き直せます!
const p = x => 0.2 - (0.2**2 - x**2)**0.5;
が描けました!

あとはこれを5回繰り返せばよいです。
繰り返すには、以下のようなのこぎり波(sawtooth wave)を入力しましょう。
のこぎり波を と置きます。
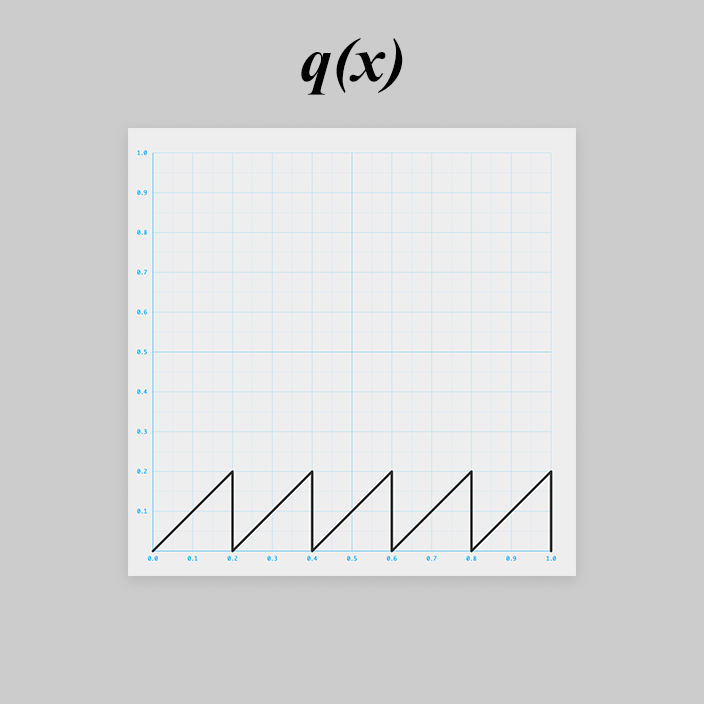
JavaScript に直すと、
const q = x => x % 0.2;
ですね!
と
を合成すると、
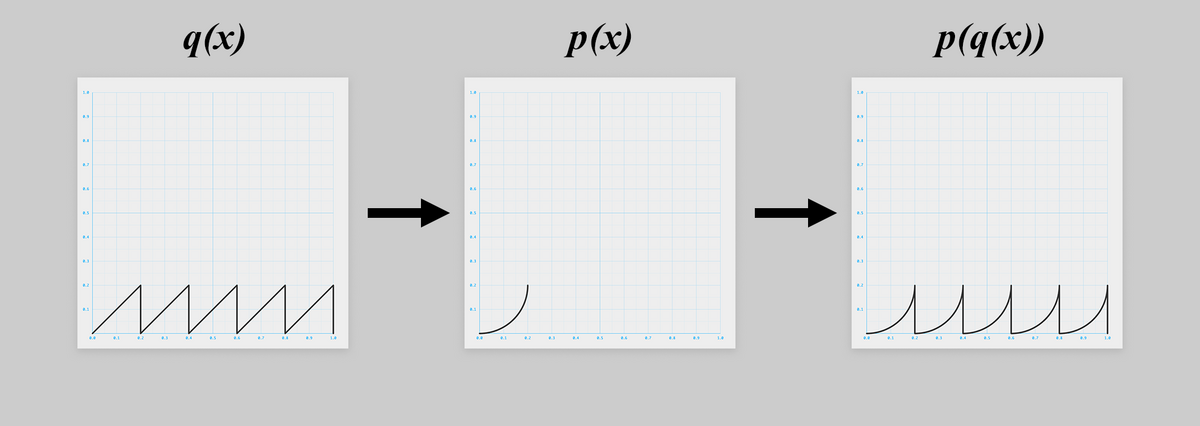
無事 つまり
ができました!
const p = x => 0.2 - (0.2**2 - x**2)**0.5; const q = x => x % .2; const g = x => p(q(x));

f(x) に g(x) を足す

準備は整いました。
と
を足し合わせましょう。
export default x => { const f = x => (5 * x | 0) / 5; const p = x => 0.2 - (0.2**2 - x**2)**0.5; const q = x => x % .2; const g = x => p(q(x)); return f(x) + g(x); };
さて、後はコードゴルフをするだけ、と思いきや
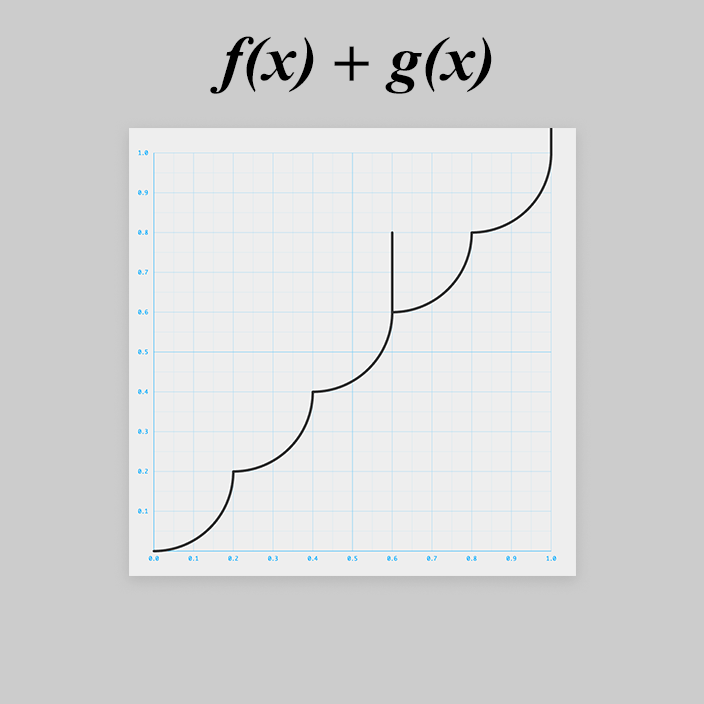
大変です!
と
で上に飛び出ちゃいました。

浮動小数点の誤差っぽいです。
const q = x => x % .2;
を
const q = x => 5 * x % 1 / 5;
と書き直してみましょう。
ちょっと文字数が長くなってしまいましたが直りました!

これと同様、 も
const f = x => (5 * x | 0) / 5;
ではなく
const f = x => (x / 0.2 | 0) / 5;
と書くと、今度は で下に飛び出てしまうので注意しましょう。

浮動小数点の誤差、厄介ですね。
ちなみに、この浮動小数点の誤差でグラフがおかしくなる現象は、例えば
graph.js の 194 行目をMath.fround()を使い以下のように修正するなどで回避できるかな、、、と思いましたが(改善はしたものの完全には)できませんでした。
そこで、浮動小数点の誤差も回避してください!というルールにしちゃいました笑

さて、浮動小数点の誤差の問題を回避したコードをさらに短くしていきましょう。
Let's CODE GOLF!
export default x => { const f = x => (5 * x | 0) / 5; const p = x => 0.2 - (0.2**2 - x**2)**0.5; const q = x => 5 * x % 1 / 5; const g = x => p(q(x)); return f(x) + g(x); };
と
を展開します。
export default x => { const f = x => (5 * x | 0) / 5; const g = x => 0.2 - (0.2**2 - (5 * x % 1 / 5)**2)**0.5; return f(x) + g(x); };
と
も展開します。
export default x => { return (5 * x | 0) / 5 + 0.2 - (0.2**2 - (5 * x % 1 / 5)**2)**0.5; };
return や不要な空白などを省略します。
export default x=>(5*x|0)/5+.2-(.04-(5*x%1/5)**2)**.5
ちょっと整理します。
export default x=>(5*x|0+1)/5-(.04-(5*x%1/5)**2)**.5
もうちょっと詰めれるような気はしますが、これまでの作戦①では44文字の達成は難しそうです。
一旦諦めて、作戦②を試しましょう。
コードゴルフでは複数のアプローチを並行で試すのが大事です!
作戦② 引き算
さて、ちょっと頭を切り替えて、今度は引き算で考えてみましょう。

グラフにするとこうなります。
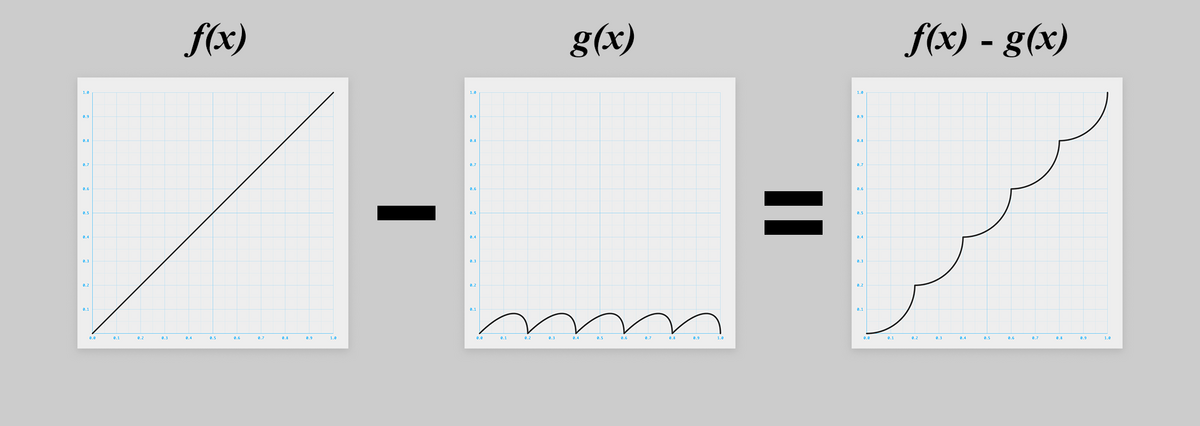
でもこの 、答えがわかってるので描けますが、頭ではちょっと想像しづらいですね。
は図形的に考えることにしましょう。
f(x) を考える
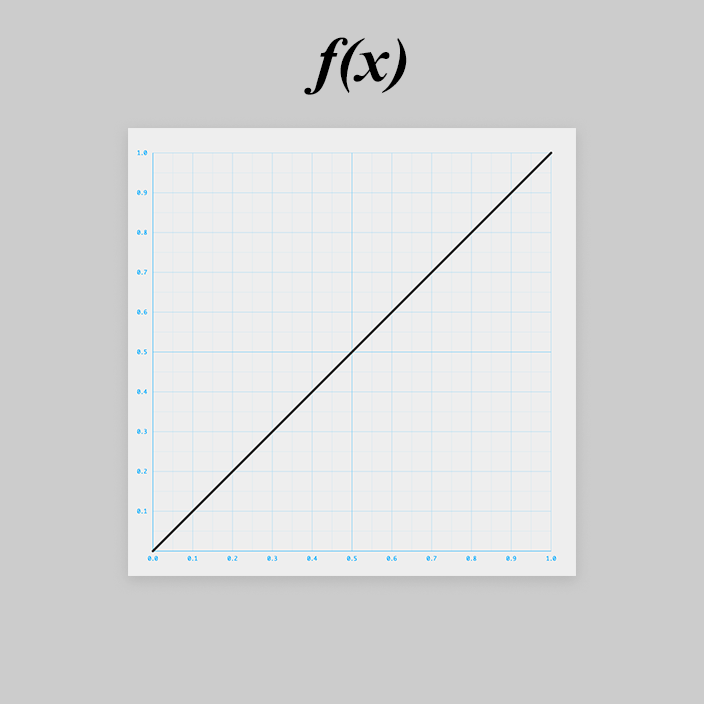
は超簡単。シンプルな一次関数です。
const f = x => x;
g(x) を考える
前述の通り のグラフはこうです。
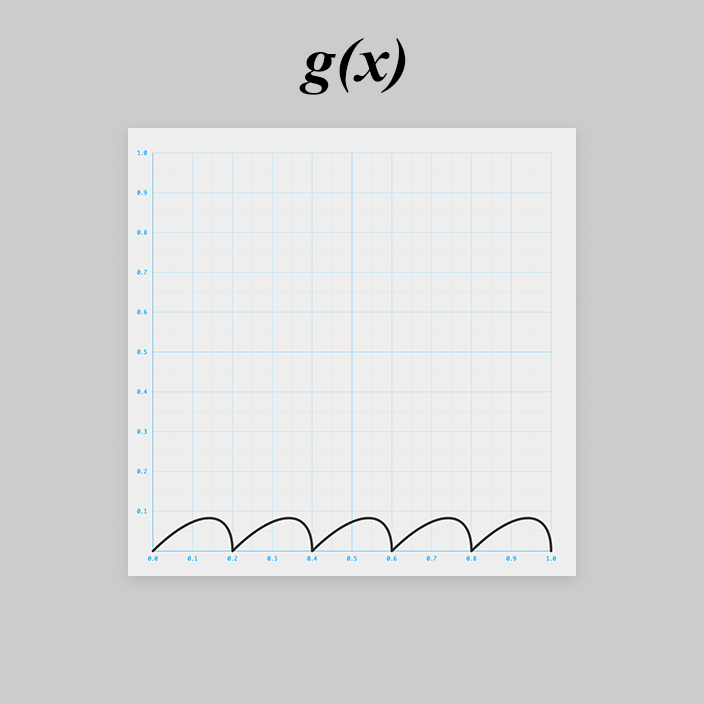
が、頭で想像しづらいので図形的に考えます。
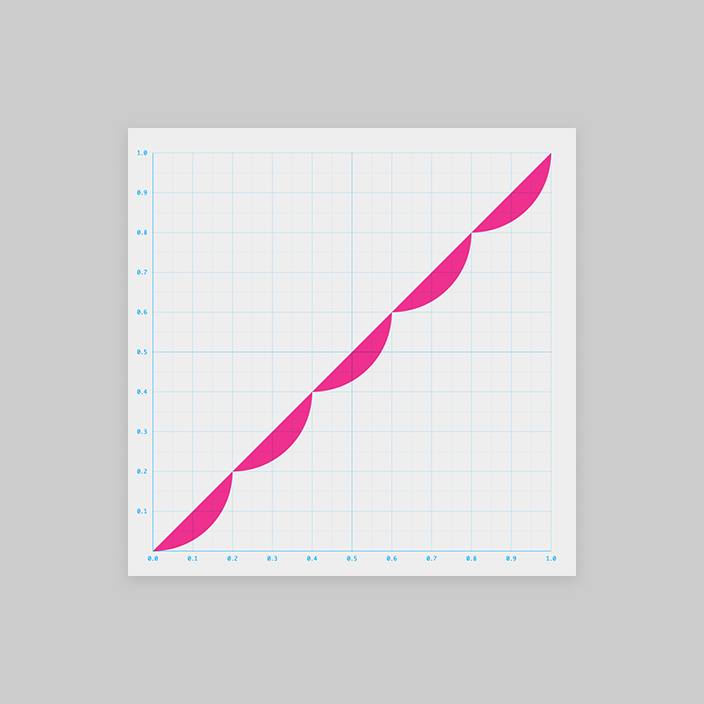
作戦①のときと同様、1周期分を考えましょう。
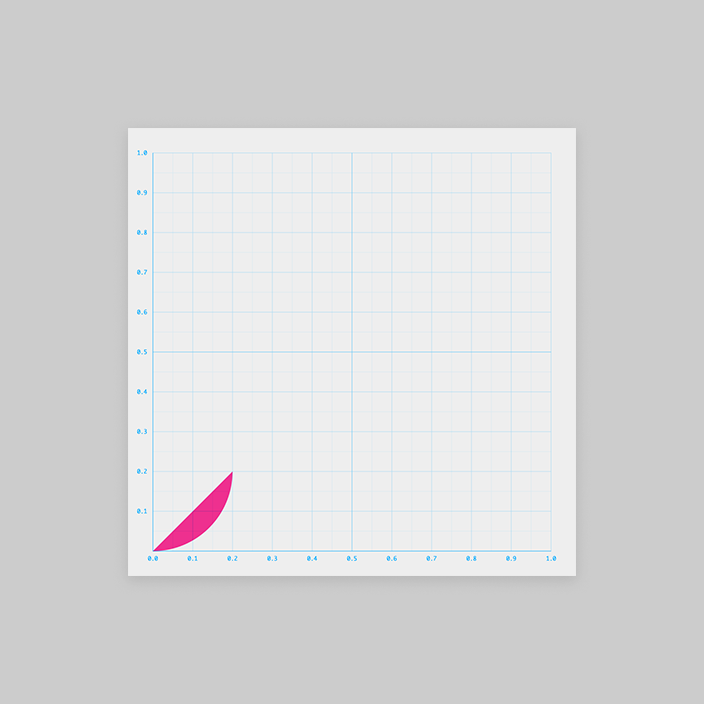
すると、これも2つの図形の引き算で表せそうですね!
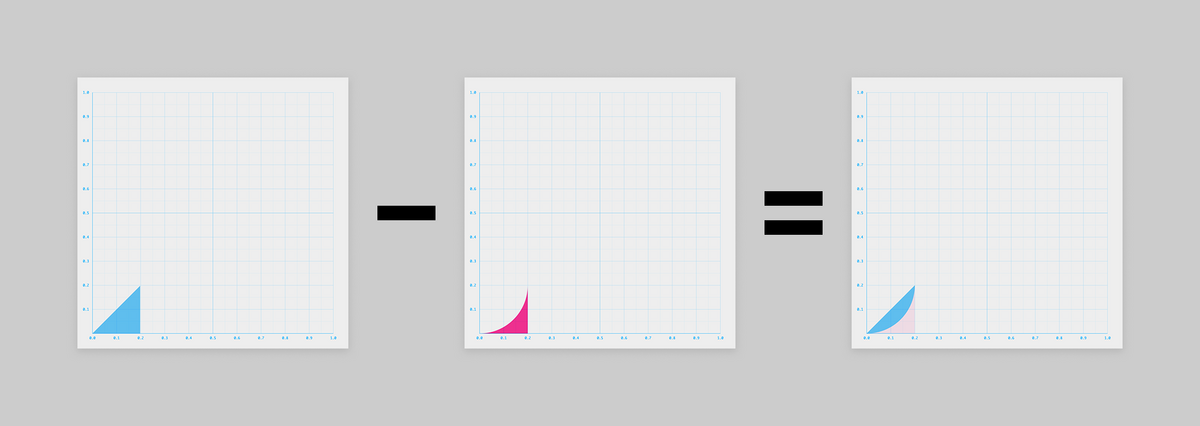
青い三角形は (の一部)


そして赤い引く方の図形は、、、見覚えがありますね!
そう、作戦①の です。
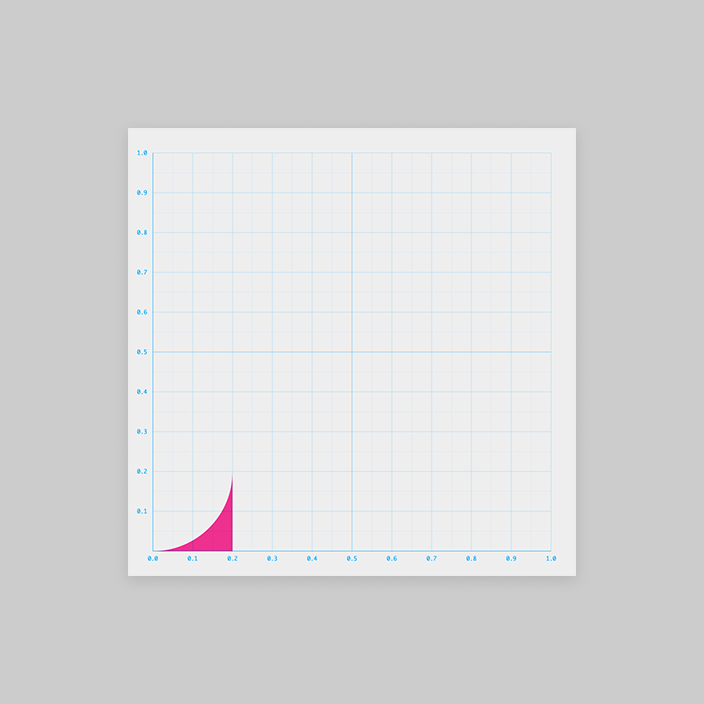

グラフで考えなおすと

またまた作戦①に登場したのこぎり波 を使って周期的にすると、
ができました!

さぁ、いよいよ JavaScript で書いていきましょう!
f(x) から g(x) を引く

export default x => { const f = x => x; const p = x => 0.2 - (0.2**2 - x**2)**0.5; const q = x => 5 * x % 1 / 5; const g = x => q(x) - p(q(x)); return f(x) - g(x); };

を展開します。
export default x => { const p = x => 0.2 - (0.2**2 - x**2)**0.5; const q = x => 5 * x % 1 / 5; const g = x => q(x) - p(q(x)); return x - g(x); };
も展開します。
export default x => { const p = x => 0.2 - (0.2**2 - x**2)**0.5; const q = x => 5 * x % 1 / 5; return x - q(x) + p(q(x)); };
と
も展開します。
export default x => { return x - (5 * x % 1 / 5) + 0.2 - (0.2**2 - (5 * x % 1 / 5)**2)**0.5; };

return や不要な空白を省略します。
export default x=>x-(5*x%1/5)+.2-(.04-(5*x%1/5)**2)**.5
(5*x%1/5) が2回登場するので、(x=5*x%1/5) で一回で済ませます。
export default x=>x-(x=5*x%1/5)+.2-(.04-x**2)**.5
(今回に限っては) 5*x%1/5 は x%.2 と書き直しても浮動小数点の誤差の影響もなさそうです。
export default x=>x-(x=x%.2)+.2-(.04-x**2)**.5

x=x%.2 を x%=.2 とします。
export default x=>x-(x%=.2)+.2-(.04-x**2)**.5

そして最後!
x**2 を x*x とすると地味に1文字減ります。
export default x=>x-(x%=.2)+.2-(.04-x*x)**.5

やった!!44文字!!!!!
ようやくたどり着きました。
長かった、、、おつかれさまでした!
応用例
今回のようなグラフを作るテクニックは実際の業務でどのように応用できるのでしょうか? 例として、アニメーションのイージング関数に使うサンプルをご紹介します!
位置のアニメーションに使ってみる
const f = x=>x-(x%=.2)+.2-(.04-x*x)**.5

- 横軸:時間
- 縦軸:縦方向の位置
とすると例えばこんな動き。
https://codepen.io/tsmallfield/pen/zYXbGKx
See the Pen JS体操 No. 1 解説用サンプル① by Tohl SMALLFIELD (@tsmallfield) on CodePen.
回転のアニメーションに使ってみる
const f = x=>x-(x%=.2)+.2-(.04-x*x)**.5

- 横軸:時間
- 縦軸:回転角度
とすると例えばこんな動き。時計の秒針みたい笑
https://codepen.io/tsmallfield/pen/NWmJqzJ
See the Pen JS体操 No. 1 解説用サンプル② by Tohl SMALLFIELD (@tsmallfield) on CodePen.
スケールのアニメーションに使ってみる
const f = x=>x-(x%=.2)+.2-(.04-x*x)**.5

- 横軸:時間
- 縦軸:スケール
とすると例えばこんな動き。だんだん迫ってきます笑
https://codepen.io/tsmallfield/pen/KKYEpxO
See the Pen Untitled by Tohl SMALLFIELD (@tsmallfield) on CodePen.
このようにいろいろ応用が可能です。
コマアニメーションにも使える
イージング関数以外に、
実はコマを1コマずつ進めていく処理にもまた別のグラフ を使っています。
本記事でも登場した、(周期的な)床関数ですね!
const g = x=>(5*x%1)*16|0;
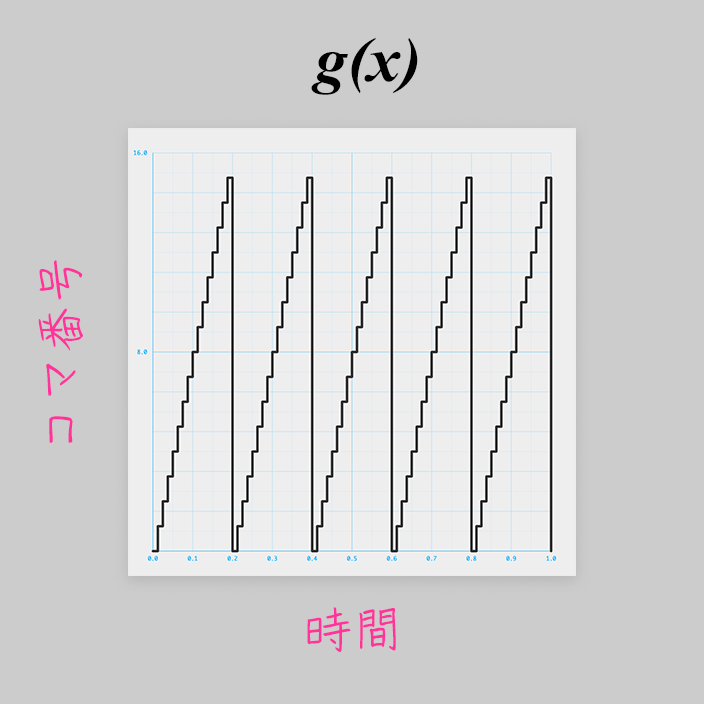

※ グラフの縦軸の範囲を 0.0〜16.0 にしています
アニメーションのループにも使える
さらにアニメーションを無限にループさせる処理にも別のグラフ を使っています。
本記事でも登場した、のこぎり波ですね!
const h = x=>x%1;

※ のこぎり刃であることがわかりやすいよう、グラフの横軸の範囲を 0.0〜5.0 にしています
アニメーションは何らかのパラメータの時間変化なので、グラフで考えると楽ですね!
イージング関数については以前こんな記事も書いています。ぜひご覧ください!
まとめ
最後まで読んでいただきありがとうございます!
44文字の解説、いかがでしたでしょうか?
実は問題を作った私も当初自力では44文字に到達できませんでした。
Math.sqrt(n) を n**.5 と書けることになぜか気づかなかったり。 は
であることは知っているのになぜ…
言われてみればそうだよな、と思うことでもなかなか思いつかない、気づかないことってありますよね。ほんと不思議です。笑
- 一つのアプローチにこだわらず、複数のロジックを比較したり
- 数学脳と JavaScript 脳をうまく切り替えてみたり
- エディタの中だけで考えず、紙と鉛筆を使ってみたり
- デスクだけでなくお風呂や電車の中などいろいろな場所で考えてみたり
など、コードゴルフの奥義がまだまだたくさんありそうですね。
そしてなにより、みなさんの回答がとても勉強になりました。
「こんなアプローチがあったのか!」とか「こんな裏技できたか!」などたくさんの刺激・気づきが得られました。複数の回答を送っていただいた方も多く、感激です。挑戦していただいた皆さま、ありがとうございました。
実際の業務でコードゴルフ自体が求められることはまず無いのですが、コードゴルフに必要な知識と技術は実際の業務でもとても重要です。言語仕様の理解を深めたり、プログラミング的な思考力を高めるのにもってこい。そしてなにより、頭の体操として面白いですよね。
今後も、実際の業務に応用できそうな、解いていて面白い問題を出していきますので
ぜひ、日々の鍛錬・息抜きに『JS体操』はじめてみませんか!
次回は、みなさまに投稿していただいた裏技的アプローチのコードをいくつかご紹介します。
想定していなかった面白回答がたくさんですよ!
お楽しみに!!
お知らせ
次回以降の「解説ブログ」や「JS体操の問題」のお知らせが気になる方はこちらにご登録ください。
公開次第、ご連絡します!
実は先日、Perl のコードゴルフコンテストもカヤック主催で開催されました。
こちらも面白いのでぜひご覧ください!
techblog.kayac.com
そして、カヤックではコードゴルフが大好きな新卒&中途エンジニアも募集しています!