
こんにちは。技術部平山です。
2019/06/25に4社合同のLT大会があったのですが、 お客さんがIT業界の方々ということで何を話していいかわからず、 たまたま趣味でやったことをそのまましゃべってしまいました。 今回の記事は、このデモの追尾計算に絞って説明するものです。
なお、このデモのパーティクル計算部分は参考にしないでください。標準のParticleSystemを使いましょう。完全に趣味です。
ちなみに、このデモに含まれる追尾以外の要素についても順次記事にしていきます。
- 球面分布とベクトルの回転
- カメラ制御
デモ概要
デモはWebGLで動くものを用意しました。 ソースコードはgitHubにあります。
右上のゲージは処理負荷です。左の数字が最近60フレームの平均時間、右の数字が最近60フレームの最大時間です。 平均が16に収まっていれば、60フレーム毎秒で気持ち良く動いていることを示します。
Fireボタンを押すと、ビームが敵に向かって飛んでいきます。 Fire16ボタンを押すと、ビームを同時に16本発射します。
Threadボタンを押すと、スレッドによる並列化が有効になりますが、WebGLではスレッドが使えないので効きません。 また、パーティクル数はStandaloneでは10万、それ以外は2万に設定してあります(ビームをたくさん出すとパーティクルが消えて寂しくなります)。 MacBook Pro 2018では、PCビルドで10万パーティクル出しても、ほぼ60fpsを保てました。 が、標準のパーティクルを使えばもっと大量に出せますので、どうでも良いことです。
このデモを作った動機
ずいぶんと昔の話ですが、2003年にANUBIS というゲームが発売されまして、そのビームや雪、煙といった表現に私は衝撃を受けました(動画は検索するといっぱい出ます)。 パーティクル表現がかっこ良かったのです。
だいたい同じ頃に私もビームその他を出す仕事をしていて、 ビームが命中した際の火花や雪の粒などで パーティクル表現を試みたりもしていたのですが、 「パーティクル前提の表現を模索する」というところまでは踏み込めませんでした(新卒一年目でしたし)。
その後、GDCで「これからはシェーダで100万個パーティクル出せるぜ」的な講演 を聞いて、「ビームの本体含めて丸ごとパーティクルで行けるんじゃない?」と思うようになりましたが、 いろいろそれどころじゃなかったので、何もしないまま時が過ぎました。
そして今回、 「全くゲームを知らない人に5分で話してゲーム作りを感じてもらうネタ」 を考えていた時に、ふとビームを思い出したのです。
追尾の実装クラス
今回説明するビームの追尾を行うのは、 Beamクラス です。Beam自体は何も描画しないので、MonoBehaviourではありません。
今回はビームを線ではなく、内部的には動く点として実装しました。 移動しながら経路上にパーティクルを置いていった結果、線に見える、 というイメージです。当たり判定は先頭にしかありません。 ゲームによっては途中や末尾にも当たり判定が欲しいこともあるでしょうが、 曲がる場合は履歴が必要になって面倒なので、今回はやめました。
持っているデータのうち毎フレーム変化するのは、
- 位置(position)
- 速度(velocity)
- 動作中か否か(time >= 0で判定)
です。Update()で積分して更新します。不変のパラメータとしては、
- 方向転換用加速度の最大値(maxCentripetalAccel)
- 推進加速度(propulsion)
- 空気抵抗(damping)
があります。追尾を行い、速度を一定に保つためのパラメータです。
さまざまな追尾の手法
敵を追尾する方法はいくつかあります。主なものは以下の3つでしょうか。
- 縦横の角度を独立に動かす
- Quaternion(クォータニオン)の補間を使う
- 加速度を加えて曲げる
縦横の角度を独立に動かす
一番素直なのは、 縦角度(仰角/俯角。オイラー角のx)と、横角度(方位角。オイラー角のy)を バラバラに操作する方法です。数学の知識が最も少なくて済みます。
今自分から見て標的が上20度、左40度に見えるとしましょう。 毎フレーム角度を変えられる量を決めておきます。 例えば「縦は2度、横は3度」としましょうか。 次のフレームでは縦角度を18度に、横角度を左37度に修正します。 また次のフレームでは角度を測り直し、また角度を修正します。 これを繰り返します。
この方式は「地面と空の方向がはっきりしているゲーム」であれば扱いやすく、 ゲームバランスの調整もしやすいという利点があります。 例えば「縦方向はあまり追尾しないが横はよく追う」という調整をすることで、 「ジャンプで避けやすく走っても避けられない」といった性質を出すことができます。
しかしながら、宇宙ゲームや戦闘機ゲームのように「上も下もない感じ」のゲームでは問題が出ます。 だいたい真横を向いていれば(縦角度が0付近なら)問題ないのですが、 真下や真上に近づくとおかしくなるのです。
今、縦角度が89度で、横角度が南(-90度)を向いているとしましょう。これを北(+90度)に向けるには、 縦に2度回すのが一番近道です。しかし、縦横独立で計算すると、 縦角度は同じ89度なので変えられず、横角度は180度回すことになります。毎フレーム3度なら60 フレームかかってしまうのです。
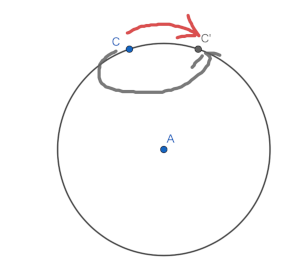
なので、ゲームデザイン的に縦角度と横角度を分けたい、という話でなければ、 この方法はおすすめできません。 角度を経由するとどうしても三角関数を経由して計算するので、負荷も大きくなります。
Quaternion(クォータニオン)を使う
「今向いている方向」は縦角度と横角度の2つの角度で表せますが、 別の表現としてQuaternion(クォータニオン) というものがあります(rは長音にするという規約に従えばクォターニオンの方がいいと思うなあ。余談)。
これを使えば先程の例で「真上を通って逆側へ最短で回す」ことができます。 この場合は、「毎フレーム2度回せる」のように縦と横を分けない角度で済むので、パラメータが減って楽です。
ただし、UnityのQuaternion の機能はかなり少ないですし、使い方を紹介する記事もあまりありません。 クォータニオンは大変便利ですので、いずれこのブログでも取り上げますが、 今回は別の方法を用います。
速度ベクトルに加速度を加える
これが今回採用した方法です。 詳細を説明します。
追尾計算の詳細
Beamクラスは元々速度ベクトルvelocityを持っているので、 これに加速度ベクトルを加算して方向を曲げます。
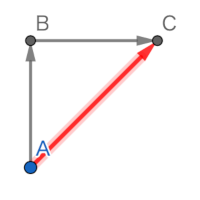
今Aにいて真北Bを向いているとして、敵が北東Cにいる場合、 移動方向(ベクトルAB)に東(ベクトルBC)を足せば、北東(AC)に向きますよね? そういうイメージです。
コードは以下です。
var toTarget = target - position; var vn = velocity.normalized; var dot = Vector3.Dot(toTarget, vn); var centripetalAccel = toTarget - (vn * dot); var centripetalAccelMagnitude = centripetalAccel.magnitude; if (centripetalAccelMagnitude > 1f) { centripetalAccel /= centripetalAccelMagnitude; } var force = centripetalAccel * maxCentripetalAccel; force += vn * propulsion; force -= velocity * damping; velocity += force * deltaTime;
まず、敵へ向かうベクトルを得ます(toTarget)。
「AからBへ向かうベクトルはB-A」です。
ベクトル演算に不慣れな方は「B-AはAからB!AからBはB-A!」と声に出して
唱えると良いでしょう。クセになると間違えません。
次に、「速度を敵方向に曲げるベクトル」を計算します。 図で書けばこうです。
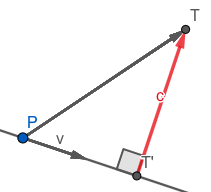
図中のPが今の位置、Tが敵の位置で、 vが速度ベクトル、という時に、図中のcが求めるベクトルです。 まず速度ベクトルを正規化したものを用意します(コード中のvn)。 そして、敵へ向かうベクトルをvnに射影します。
射影、というのは文字の通り「影を写す」ことで、 図のT'を求めることです。下の図をご覧ください。
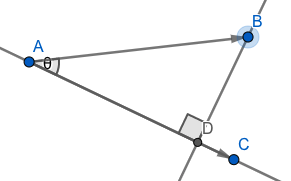
図中のベクトルABを、ベクトルACに射影してできる 点Dの位置が欲しい、という場合、
cosθ = Dot(AB, AC) / |AB||AC|
で、
cosθ = |AD|/|AB|
なので、
|AD| = cosθ*|AB|
= (Dot(AB, AC) / |AB||AC|) * |AB|
= Dot(AB, AC) / |AC|
となります。先程の話で言うvにあたるACを前もって正規化しておけば、 |AC|での割り算はいらなくなります。コードで書けば、
AC.Normalize(); D = A - (AC * (Vector3.Dot(AB, AC));
となります。 Dは元のコードではcentripetalAccelに当たりますから、 これで欲しいものが得られたわけです。 あとは長さをテキトーに変えて速度に足せば、速度を曲げることができます。
この「長さをテキトーに変える部分」は以下になります。
var centripetalAccelMagnitude = centripetalAccel.magnitude; if (centripetalAccelMagnitude > 1f) { centripetalAccel /= centripetalAccelMagnitude; } var force = centripetalAccel * maxCentripetalAccel;
やけに長いcentripetalAccelという変数は、
曲げるために加える加速度を表しています。
centripetalというのは「中心を向いた」という意味です。
ひもがついた重りをグルグル回す時、重りが飛んでいかないのは
ひもが重りを中心方向に引っぱっているからで、
これを向心力(centripetal force)
といいます。ここでは直接加速度で扱っているので「力」でなく「加速度」、
ということでAccelをつけていますが、同じものです。
さて、centripetalAccelの長さ(magnitude)が1以上なら、長さを1に正規化します。 1未満ならそのままにします。 そしてmaxCentripetalAccelを掛けます。これで 「長さがmaxCentripetalAccel以下ならそのまま、以上なら長さをmaxCentripetalAccelにする」 という処理になります。 つまりmaxCentripetalAccelは「曲げる力の大きさの最大値」ということになります。
パラメータを扱いやすく
さて、前の二つの手法と違って、「毎フレームこれくらい曲げる」を 角度でなく加速度で定義していますので、このままでは直感的ではありません。 なので、外からは別のものを受け取っています。
public void Emit( Vector3 position, Vector3 velocity, float speed, float curvatureRadius, float damping) { this.position = position; this.velocity = velocity; // 速さv、半径rで円を描く時、その向心力はv^2/r。これを計算しておく。 this.maxCentripetalAccel = speed * speed / curvatureRadius;
maxCentripetalAccelは内部で計算されており、外からは見えません。
外からもらうのはcurvatureRadius、日本語で言えば「曲率半径」で、
要するに、「半径何メートルの円の感じに曲がれるか」を表します。
小さいほどキビキビ曲がれてよく追いかけられるわけです。
例えば、標的との距離が100mの時に、あさっての方向を向いていても当たって欲しい、
というのであれば、曲率半径は50m以下である必要があります。
そうでないと、地球の周りを回る月のように永遠に当たりません。
「1秒あたりの角度」よりも「追尾の鋭さ」がわかりやすいと思うのですが、いかがでしょうか。
そして、向心力は速度の二乗/曲率半径で求まります。
速さを一定に保つ
今回のデモでは、ビームの速さは一定です。これを実現しましょう。
ところで、今「速さ」と言いました。「速度」とは区別しています。 「速さ」は「速度ベクトルの長さ」のことです。 コード中ではspeedで表し、速度ベクトルはvelocityです。 この「速さ」と「速度」の使い分けは比較的メジャーなものかと思います。
さて、ビームが曲がっても速さは一定にしたい、というのが今回の要望です。 しかし、速度ベクトルに足し算をすれば、当然速さは変わってしまいます。 そこで、速さを一定にするために、dampingによって毎フレーム速度を落とし、 さらにパラメータとして与えたpropulsion(推進力)によって毎フレーム加速を加えています。
「速度ベクトルを正規化しちゃえばいい」 と思われるかもしれません。それでもいいと言えばいいのですが、 今回はせっかくなので「力を与えて制御し、位置と速度は直接いじらない」 という物理シミュレーションの基本に乗せてみました。
例えばdampingに0.1が入っていれば、速度は1秒のうちに90%に減速します。 これによって、曲げたことによる加速の影響はどんどん消えていきます。 そして、速度を一定に保つために、推進力propulsionによって、速度方向に加速するのです。 いずれ、抵抗と推進が釣り合って速度が一定になります。 ミサイルが燃料を燃やして進むのがpuropulsionで、空気抵抗がdampingと考えると、 現実の物理的な解釈がしやすいかと思います。
force += vn * propulsion; // 推進力 force -= velocity * damping; // 空気抵抗 velocity += force * deltaTime; // 速度積分
物理シミュレーションの枠組みから逸脱しないので、 何らかの物理シミュレーションのフレームワークに乗っかっていて(Rigidbodyとか) 積分を自分で書けない時でも使えます。
パラメータを使いやすく
先程の曲率半径と同じく、外から直接推進力を与えるのは不便なので、 違うものを与えています。
public void Emit( Vector3 position, Vector3 velocity, float speed, float curvatureRadius, float damping) { //...省略... this.propulsion = speed * damping;
単純に「速さ(speed)」を与え、 これとdampingからpropulsionを計算しています。
dampingによる抵抗力は-velocity * dampingで、
velocityの大きさがspeedになった時にこれを打ち消せば良いので、
propulsionにはspeed * dampingを設定すれば良いわけです。
今回の場合dampingはいくらにしても大差ないので、外から与えず中でテキトーに 0.1などと入れておけば良いのですが、まあそのへんは細かい話ですね。
まとめ
今回紹介した追尾の計算の利点は、
- 普通のベクトル演算だけで書ける
- クォータニオンも行列もいらない
- 三角関数が出てこない
- 物理シミュレーションの枠組みから外れない
といったものです。とりわけ「普通のベクトル演算だけで書ける」 ことは、「2Dでも3Dでもコードがほとんど同じ」という利点にもなります。 実際、Vector3をVector2に置き換えるだけで、そのまま2Dゲームでの追尾処理になるのです。
欠点は、
- 厳密には等速を保てない
- 空気抵抗という本来いらないパラメータが介在している
- ベクトル操作に慣れていないとわかりにくい
- 曲率半径が小さすぎると曲げすぎて落ちつかず軌道が揺れる
といった感じになるでしょうか。
なお、「決まった時刻に必ず当たるように追尾したい」 という場合にはまた違った手法があると思います(24ページあたりから)。 今回は「当たるとは限らず、追尾性能に限りがある」という条件での計算です。