画面をクリックするとwebGLサンプルに飛びます。動画もあります。
こんにちは。技術部平山です。
最近たまたま紙吹雪っぽいエフェクトを作る機会があったので、これを、 「これまで書いてきた基本的な技法を組み合わせる応用例」という位置付けで紹介しようと思います。
コードはgithubに置いておきました。 また、ちょろっと入れて試したい方のために、パッケージも用意してあります。
使い方
パッケージをつっこんで、中にあるConfettiというプレハブをどこかに置けば、何か絵が出ます。 デフォルト設定だと、だいたい100くらい離れた所から見ないとよくわからないので、 カメラからの距離には注意してください。
所詮サンプルなので、それほどのカスタマイズ性はありません。 パラメータの変更で済まない場合は、改造するなり自作するなりしてください。 自作の方がおすすめです。それなりにいろんな知識を試されると思います。
作るために必要な知識
使う知識の分野はだいたい以下の感じです。
- 3Dベクトル演算
- 質点物理(高校でやる奴)
- クォータニオン少し(積分含む)
- スキニングを用いたインスタンシング的描画
過去の記事で関連するものとしては、
あたりがあります。これらの記事の内容を理解していないといけない、 というわけではありませんが、かなり深くつながったお話にはなります。
一枚の紙切れから
まず、一枚の紙切れの挙動を作る所から始めましょう。 それができてしまえば、あとはたくさん出すだけです。 今回は「紙切れと紙切れはぶつからないし影響し合わない」 としているので、紙切れが増えた時に問題になるのは処理速度だけです。 しかし処理速度についても、今回は「すぐできる範囲」でだけ手を打ち、 手間がかかる所(逆に言えば面白いところ)は、また今度にとっておきます。
質点物理
物理シミュレーションの中で一番簡単なのは、 質点のシミュレーションです。
大きさがないので、回転を考える必要がありません。
大きさがないので、形という概念がそもそも必要ありません。
Unityに入っている剛体(rigidbody)物理 に比べれは、遥かに簡単に処理することができます。 質点でできることに剛体を使うのは無駄ですから、まずは質点でできないかを考えるべきなのです。
運動方程式の実装
さて、質点の物理は簡単に言えば以下のコードで書けます。
accel = force / mass; velocity += accel * dt; position += velocity * dt;
これは運動方程式をコードにしたもので、 力を質量で割って加速度を出し(1行目)、加速度を積分して速度を出し(2行目)、 速度を積分して位置を出します(3行目)。
積分にはいくつか手法がありますが、上のコードは最も簡単で使い勝手がいい 半陰的オイラー法(英語)です。 2行目と3行目を逆にすると、基本のオイラー法になりますが、 実用にはなりません。 速度を先に更新して、それをすぐ位置の更新に使う、という半陰的オイラーの方が 圧倒的に使えます。
質量の省略
今回の応用では、質量を1に固定することにました。 力を質量で割る必要がなくなって楽だからです。 また、個別に質量を持つ必要がなくなってデータ量が減ります。 これによって上のコードの1行目が不要になり、いきなり加速度が計算できます(概念的には1で割っていますが)。
velocity += accel * dt; position += velocity * dt;
かかる力
では紙切れにはどんな力がかかるでしょうか。今回は二つの力をかけています。
- 空気抵抗
- 重力
しかし、質点の状態では空気抵抗はかけようがありません。大きさがゼロなので、 空気抵抗はゼロのはずです。が、ウソをついて入れます。 速度に比例した強さでブレーキがかかるとしましょう。
accel = gravity + (velocity * -resistance);
こうですね。重力は定数で良いでしょう(地球からの距離が大きく変われば変化しますが、紙吹雪ですからね)。 例えば(0f, -9.81f, 0f)みたいな感じのベクトルになります。 今回は好きな方向に落とせるように、Unityの設定を取らずに、 自分で与えられるようにしています。Z方向に落ちたってかまいません。
空気抵抗は、速度ベクトルvelocityに、抵抗の強さresistanceを掛けて力にします。 この時にマイナスをつけるのは、「速度の逆向き」の力が発生するからです。
拡張の選択肢二つ
さて、とりあえず単純な質点物理でできることはここまでなんですが、 はっきり言ってこの段階では紙切れには見えません。 一切回転せずに、放物線を描いで落ちるだけです。 これに何を足したら、紙切れっぽくなるの?ということを考える必要があります。
ここで望む動きを得るために行う拡張には、選択肢が二つあります。
- 剛体物理に切り換える
- 質点物理のままどうにかする
剛体物理は回転を扱えますから、剛体物理にすれば100%解決します。 問題は、理屈が面倒くさくて計算も重いことです。 UnityのRigidbodyを使えば実装そのものはしないで済みますが、 最終的に千枚とか1万枚とか出したいと考えると、 ridigbodyコンポーネントをつけたgameObjectをその数置くのは ちょっと辛いでしょう。
そこで今回はもう一つの道を行きます。 質点物理のままでどうにかしましょう。 質点物理を拡張する場合の常道は、「質点を増やすこと」です。 2個あれば結んで線が表現でき、3個あれば三角形が表現できます。 多数をつなげば立体だって表現できます。
まずは一番簡単な2個で行きましょう。
二個の質点
とりあえず、位置と速度を2個用意して、バラバラに積分します。
accel0 = gravity + (velocity0 * -resistance); accel1 = gravity + (velocity1 * -resistance); velocity0 += accel0 * dt; velocity1 += accel1 * dt; position0 += velocity0 * dt; position1 += velocity1 * dt;
これけだけでは、単にバラバラに点があるだけです。 望む結果を得るには二つのことをやる必要があります。
- 2つの点の間の関係を保つ
- 2つの点でかかる力が変わるようにする。
2点が何の関係もなくバラバラに動いたら大変ですよね。 1毎の紙切れの中の2点ですから、何らかの関係が必要です。
そして、2点にかかる力、ひいては加速度が違ってこないと、両方が同じ動きをするだけなので 2点にした意味がありません。片方は早く下に落ちるが、片方はなかなか落ちない、 みたいなことが起こるように細工する必要があります。
拘束関係
まずは関係を作ります。
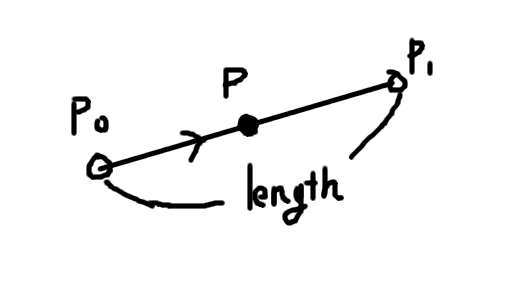
2点は一つの紙切れの中のとある代表点です。 例えば左端と右端、みたいな感じでしょう。 今紙切れが変形しないのであれば「2つの質点の距離は不変」です。 これを強制するために、位置は2つ持たず1個だけにし、 点0から点1へ向かうベクトルと、点の距離をフィールドに持っておきます。 ベクトルは前方向を表すということでforward、距離は紙切れの長さということでlengthとしておきましょう。 すると、更新処理はこうなります。
// 二点を中心位置から生成 var position0 = position - (forward * (length * 0.5f)); var position1 = position + (forward * (length * 0.5f)); // 積分 accel0 = gravity + (velocity0 * -resistance); accel1 = gravity + (velocity1 * -resistance); velocity0 += accel0 * dt; velocity1 += accel1 * dt; position0 += velocity0 * dt; position1 += velocity1 * dt; // 二点の中心を位置として保存 position = (position0 + position1) * 0.5f; // forwardは2点の差で更新 forward = (position1 - position0).normalized;
フィールドはpositionだけになったので、毎フレームpositionとforward、lengthから 2点を生成します。position0とposition1はローカル変数なのでvarです。
そして、積分が終わった後で2点の平均をpositionに保存し、 今の位置からforwardを再計算します。
速度がウソついてるのを直す(Verlet(ベレ)法)
よく見てみると、現状速度がウソをついています。 バラバラに積分していれば問題ないのですが、2点の距離を保つ計算をするために 無理矢理位置を動かしてしまったので、速度が合いません。
例えば、x=0から速度5で1秒進めばx=5に着きますが、 ここで無理矢理xを4にされてしまったらどうでしょう。 速度には5と書いてありますが、実際には4しか進んでいないのです。
この状態は不安なので(放っておいてもいいのかもしれず確証はない)、解消しておきましょう。 簡単な方法は、積分をVerlet(ベレ)法 に変えることです。
簡単に言えば、速度を覚えておくのをやめます。 その代わり、前の位置を追加で覚えておくようにします。積分は、
var newPosition = position + (position - prevPosition) + (accel * (dt * dt * 0.5f));
prevPosition = position;
position = newPosition;
となります。(position - prevPosition)は、1フレームに動いた量なので、 今までの(velocity * dt)にだいたい相当します。
こうすると、速度を覚えておかないので、位置を無理矢理いじってもウソの状態になりません。 Verlet法の利点は他にも安定性や精度などあるのですが、 Verlet法の利点を最大に活かすためには「フレームとフレームの間の時間が一定」「速度が力に影響しない」 という条件が必要で、今はどちらも満たされません。 フレームの間の時間が変わる場合でも精度を上げたい場合には、 A Simple Time-Corrected Verlet Integration Method に良い解説があります(やったことないですけどね!)。
空気抵抗を工夫する
さて、次は2点にかかる力が変わるようにしましょう。 2点で位置がずれれば、それによって回転運動が発生します。
今、紙きれは曲がっているものとします。 そして、空気抵抗は紙切れの法線方向にかかるものとします。
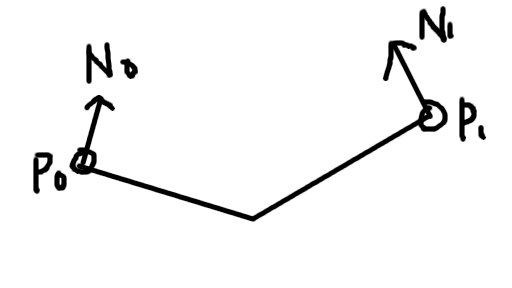
2点で法線が異なれば、かかる空気抵抗も違ってくるはずです。
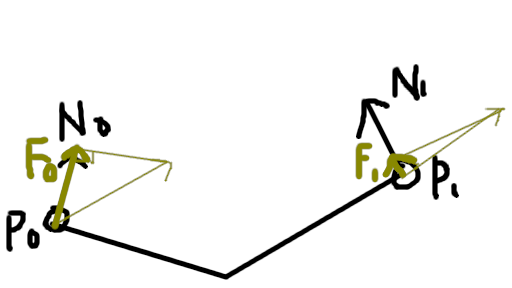
速度ベクトルをそれぞれの法線に射影したものがそれぞれかかる力となり、 図ではそれがF0とF1です。さっきVerletにしてしまったので速度ベクトルはありませんが、 近似しちゃいましょう。
velocity0 = (position0 - prevPositon0) / dt;
で良しとします。dtは毎回変わるので、今回のdtで割っちゃうのはウソなんですが、 気にないことにしました。安定して動いてればそんなに変わりませんからね。
あとは法線がnだと仮定すると、
var dot = Vector3.Dot(n, -velocity); var accel = n * (dot * resistance);
と加速度が計算できます。内積が負、つまり射影した時に 法線と逆を向く場合もそのままでかまいません。 これは裏から空気がぶつかった、ということで概念的には 法線をひっくり返してから内積を計算することになるわけですが、 結果は同じになります(先にnを反転させればdotも反転し、掛ければ同じになる)。
法線を計算する、ためにクォータニオン
あとは法線です。とはいえ、今の状態だと、点が2個の1次元世界なので、 「上ってどっち?」という状態です。そこで、「この紙切れにとっての上」を 定義してやる必要があります。 そのための道具がクォータニオンです。
クォータニオンである変数rotationが姿勢を持っているとすれば、 先程用意したforward、つまり前方向ベクトルは、
var forward = rotation * new Vector3(0f, 0f, 1f);
で出てきます。もうforwardを持つ必要はありませんね。 上方向、右方向はそれぞれ、
var up = rotation * new Vector3(0f, 1f, 0f); var right = rotation * new Vector3(1f, 0f, 0f);
です。紙がXZ平面で、法線がy軸であるとすれば、法線はこのupです。 これを2点で別々に修正して、紙が曲がっていることを表現します。 例えば、点0の法線はforwardの0.1倍を足し、 点1の法線はfowardの0.1倍を引く、というようにすれば、法線が2点で違ったものになります。
var up = rotation * new Vector3(0f, 1f, 0f); var n0 = (up + (forward * 0.1f).normalized; var n1 = (up - (forward * 0.1f).normalized;
2点それぞれの法線が生成できました。この0.1fは調整パラメータで、
normalBendRatioとして用意してあります。大きいほど曲がりが大きい、
ということですね。
姿勢更新
最後に、姿勢クォータニオンを更新します。 それには、forwardが計算前と後でどう変わったかを見て、 そこから回転クォータニオンを生成し、これを今の姿勢に掛け算して回します。
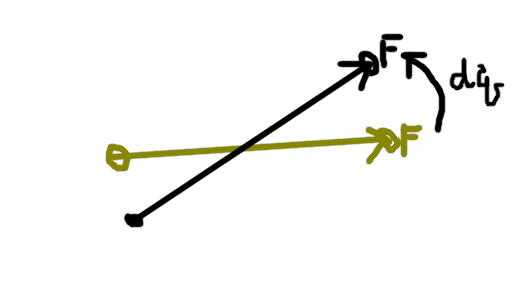
var newForward = (p1 - p0).normalized; // forward -> newForwardに向くような、回転軸右ベクタの回転を作用させる var dq = Quaternion.FromToRotation(forward, newForward); rotation = dq * orientation; // dqは時間的に後の回転だから、ベクタから遠い方、つまり前から乗算 rotation.Normalize();
今回転は1軸でしか起こらない(左右軸でしか回らない)ので、 forwardの変化具合を見れば十分です。
これどういうふうに動くの?
だいたいこんな動きをします。

紙切れの法線が垂直(地面に置いてある時のような感じ)に近いほど、 空気抵抗が大きくなるので減速します。 紙切れが立った状態になると、空気抵抗が小さいので重力でどんどん加速します。
しかし、2点で法線が違うため、縦に立った状態であっても、 2点でかかる力が異なり、落ちる速度に差が出ます。その結果紙が回転し、 立った状態からだんだん寝た状態になってくるわけです。
結果、ヒラヒラした感じで落ちてくることになります。 重力と空気抵抗のかねあい次第では、一時的に上に舞い上がったりもするので、 結構面白いです。
風について
今回の実装では風の強さも指定できます。
風の強さだけ空気抵抗の計算時に速度を補正し、 「空気に対しての相対速度」で空気抵抗を計算しています。 紙切れごとに風を少しづつ変えると、 もっとランダム感が出ていいかもしれませんが、 それをやりたければ、質量を導入してバラつかせた方が 安いかもしれません。
描画について
描画は、「紙切れごとにMeshRendererがついたGameObjectを用意する」 というようなことをやるとさすがに重いので、 今回最適化をしてしまいました。
といっても簡単で、以前紹介した「スキニングを使ったインスタンシングもどき」)を使うだけです。 SkinnedInstancingRenderer なるクラスをその記事の時に作ったので、これを使います。
そうすれば、それぞれの紙切れにGameObjectやTransformを持たせる必要がありません。 位置とQuaternionはありますから、 ここから行列を作って、Mesh.bindposes に毎フレーム詰めればそれで描画できるわけです。
行列を作るコードはこんな感じです。
public void GetTransform( ref Matrix4x4 matrix, float ZSize, // 紙の長さ float XSize) // 紙の幅 { matrix.SetTRS(position, orientation, new Vector3(XSize, 1f, ZSize)); }
Matrix4x4.SetTRS に位置、姿勢クォータニオン、スケールを与えればいいだけで簡単です。
色について
今回は色が7種類ありますが、それぞれ別のマテリアルになると速度が 遅くなってしまいます。そこで、テクスチャのアトラス化を行いました。
8x1の小さなテクスチャに8個の色を入れておいて、 それぞれの紙切れごとに違うUVを指定することで、色を換えています。

アトラス、という感じではないですが、これも立派なアトラスですよね。
例えば青であれば、Uに(3/8)+(0.5/8)=0.4375を入れ、Vはなんでもいいので0とします。 (0.5/8)は画素一個の幅の半分で、これを足すことで画素の真ん中の座標を得られます。
おわりに
どうでしょう。 ベクトル、クォータニオン、運動方程式、といった道具が使えると、 やれることが広がるので、個人的にはおすすめです。 その上でGPUの機能をうまく利用して最適化を行うと、 結構派手なことができるようになります。
もちろんUnity時代ですから、数学や最適化などの地味なことはUnityに任せて、 自分は面白いことに集中する、というのも良いでしょう。 「こんなもんShurikenで作れよ」って話です。 ただ、自分でも多少やっておくことで、「こういう知識がある奴は、この手のものが作れる」 あるいは「この手のものを作りたいと言っているのに、こういう知識がない奴は地雷」 というような判断ができるようになります。全く役に立たないということはない、と私は信じています。
なお、今回の「質点2つでヒラヒラさせる手法」を考えたのは、もう17年も前のことです。 当時参加していた製品に羽を舞い散らす演出があったのですが、 動きに物理感がなくて当時の私はあまり気に入らなかったので、 勝手に変えてしまったのでした。 新卒で会社に入って半年も経っていない頃だったせいか、 今から考えても意味のわからない情熱を持っていた気がします。 そのステージの空気の薄さや重力によってパラメータを変える、という無駄なこだわりがありました。
さて、今回扱わなかった要素に「物理計算の高速化」があります。 紙切れの挙動はそれなりに複雑で、ベクトルの正規化や、クォータニオンとベクトルの積のような重い処理が 結構な回数入っていますから、結構重いのです。 私のPC(MacBook Pro 2018)だと、フレームあたり5000枚くらいが限度です。 最近使った製品では、スマホの性能を鑑みて500枚以内に抑えました。
でも、もっと速くして、もっとたくさん出したいですよね?
最近Unity関係で流行りのDOTS(Data Oriented Technology stack) で提唱されているような手法を使えば、CPUの余っているコアを使ってもっと高速に計算できるはずです。 実はまだやっていないので、どれくらい速くできるか私も楽しみでおります。
