動画をクリックするとWebGLビルドに飛びます。 また、ソースコードはgithubに置いてあります。
こんにちは。技術部平山です。
今回は、3D空間にある物をいい具合に画面に収めるための計算について説明します。 動画では16個の球が好き放題動き回っており、 カメラはこれが全部画面に入るように追跡しています。 補間計算のために少々遅れがあってはみ出すことがありますが、 おおむね収まっていることがわかります。
17年かかってしまった...
実は、この問題に初めて出会ったのは17年も前のことです。 その時は時間がなかったので、ずいぶんテキトーな近似で良しとして、 真面目に考えることをしませんでした。
その後も数回この問題に当たる機会があったのですが、 やはりその度にテキトーな近似と手調整でその場しのぎをしてしまい、 今日に至るまでイマイチな方法しかないままで来てしまったのです。
こんなのwebにいくらでも回答あるでしょ、 と思いますし、今でも「きっとあるんだろうな」と思うのですが、 何故か見つけられていません。 つい先日またこの問題に当たった際に、 「今度は真面目にやるか」と思って考えてみたところ、 あっさり今までよりマシなものができたので、ご紹介いたします。 正直、今となっては、なんで最初にこれを思いつかなかったのかわかりません。
問題の定義
3D空間中に、画面に収めたい複数の点が存在しているとします。 これが丁度画面に収まるようにカメラのパラメータを決める、 という問題です。
動的に変化し得るカメラのパラメータは以下の3つがあります。
- 位置(Vector3)
- 向き(オイラー角ならVector3)
- 画角(field of view)
実際の状況では、このうちの何かが固定されている状態で、 他の何かを動かす、ということになります。 例えば、画角を動かさずに位置だけで合わせたり、 位置を変えずに向きと画角で合わせたりします。
さて今回は、「向きと画角を変えないまま位置だけを動かす」 方法です。つまり、求めたい数は、位置のx,y,zで3つです。
カメラが固定されている状況では、 「向きと画角を変える」方法が必要になりますが、 それはまた今度考えることにしましょう。 リアル系のゲーム(スポーツなど)であれば、 カメラは固定の方がリアルっぽいので、そちらの手法が必要になります。
まず2次元
3次元は難しいので、まずは2次元で考えます。

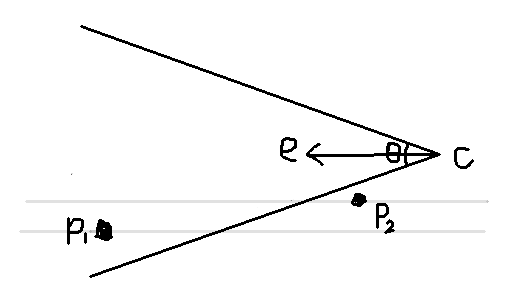
カメラ位置c、カメラの正面ベクトルe、点をとりあえずP0,P1,P2の3つ、 画角θを書いてみました。
今は向きは固定なので、eは固定です。 決めたいのはCですね。 この絵で言えばP0が視界の上端にピッタリ来るように若干下に動かし、 P2が下端に来るように前に動かし、という感じでしょうか。
さて、問題はそれをどうやって計算としてやるかです。
いらない情報を捨てる
未知数はCの座標で、2次元なので中に2つ数値があります。 ということは、式は2本あるはずだ、 ということになります。点が今3個ありますが、 点1個につき式が1つ立つとすれば、1個は余計です。
実際、図を見ればわかるようにP1はあってもなくても影響がなさそうですね。 というわけで、最初にやることは、いらない情報、つまりP1を捨てて、 P0とP2を残す作業です。あとは残った2点で式を立てて、 連立方程式を解けば、2つの解が出てくると。 そういう筋書きになるという予測が立ちます。シンプルですね。 なんで昨日よりも前の私にその筋書きが見えなかったのか、本当わかりません。
さて、集合から情報を捨てる計算といえば何でしょうか? 真っ先に思いつくのは最大と最小です。 集合の最小は1つ、集合の最大は1つなので、 最小と最大を取れば、ある集合から2個のデータを残して捨てられます。
図で言えば、上端に来そうな点P0を取ると何かが最大になって、 下端に来そうな点P2を取ると何かが最小になる、 そんな関数があれば、P0とP2以外を捨てられます。 P1以外にP3,P4,P5...が間にあっても同様に捨てられるわけです。
上下軸で捨てられる?
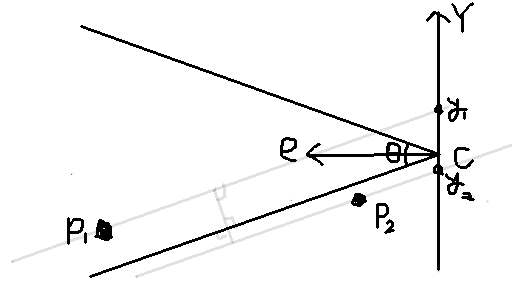
では、上下軸でしょうか。元々の問題は3次元なので、 z軸は前後軸として残し、 もう一つの軸をxかyにしましょう。上から見るか横から見るかなのですが、 画角が縦方向なのと、図に描いた時に「上はY」と言えた方がわかりやすいので、 ここでは横から見たことにして、Y軸を取ります。 eの方向がZ軸、図の上方向がY軸ということにしましょう。 つまり、Yが最大のものと最小のものを取ればいい、ということになるでしょうか。
ダメでした。
この図ではP1の方がP2より下にありますが、使うべきはP2です。 つまり、単純にY軸の位置だけでは決まりません。
では何で決まるのか?これです。
視界の下端と同じ斜めの線を 各点に引いて、それがCを通るY軸に当たる所のyの値を作り、 これで比較します。この場合は最小のものが、 視界の下端で使うべき点だとわかります。 y2はy1より下にありますから、使うのはy2を作る元になったP2ですね。
Y軸に射影した点を求めて最大最小を取る
では、y1とy2を求める方法を考えます。
とりあえず、今の段階ではP0,P1などはワールド座標で eもワールド座標ですから、 汚ない数字が入っていて扱いにくいですね。 座標変換してしまいましょう。
Cが原点、eがZ軸プラスすなわち(0,0,1)になるように P0,P1...を座標変換したとすれば、話はあっさり簡単になります。
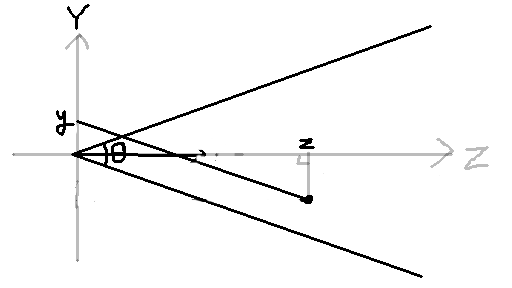
Z軸が右向きの方がわかりやすいので図をひっくり返しました。 図のPから斜め線を引いてY軸との交点を求める問題で、 斜め線の傾きa(y変化量/z変化量)がわかれば、
y = p.y - (a * p.z)
とあっさり求まります。下の斜め線の場合傾きaはマイナスですね。 全ての点についてこのxを求めて、一番小さかった奴が、 「視界で一番下に来る奴」ということになります。 上の斜め線についても同じようにyを求めて、 今度はyが一番大きい奴を探します。それが「視界で一番上に来る奴」 です。
コードにする
ここまで来ればコードにできます。
まずは全部の点をカメラのローカル座標に移してしまいましょう。 カメラのローカル座標のことを「ビュー座標」と呼ぶことが多いので、 ここでもそう呼びましょうか。
var toView = camera.transform.worldToLocalMatrix; var pointsInView = new Vector3[points.Length]; for (int i = 0; i < points.Length; i++) { pointsInView[i] = toView.MultiplyPoint3x4(points[i]); }
これでビュー座標に点が移りました。点を座標変換する時はMultiplyPoint3x4を使います。
次に、傾きaを求めます。下の線のマイナスな傾きをa0、上の線のプラスな傾きをa1とすると、
a0とa1は単純に符号違いですね。上下対称ですから。
プラスのa1の傾きは、(yの変化量)/(zの変化量)で、
これってtan(θ/2)です。
var a0 = Mathf.Tan(camera.fieldOfView * 0.5f * Mathf.Deg2Rad); // ラジアンに直す var a1 = -a0; var yMin = float.MaxValue; var yMax = -yMin; foreach (var p in pointsInView) { var y0 = p.y - (a0 * p.z); var y1 = p.y - (a1 * p.z); y0Min = Mathf.Min(y0Min, y0); y1Max = Mathf.Max(y1Max, y1); }
これでyMinとyMaxが求まりました。あとは、斜め線2本の交点がカメラの位置です。
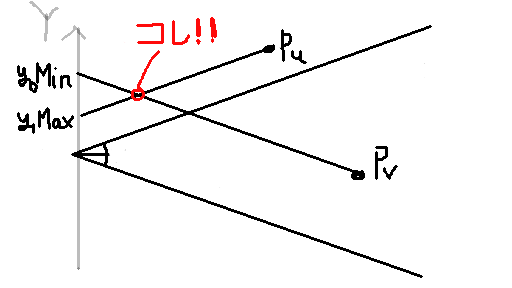
図中でu番の点であるPuからy1Maxが生まれ、
v番の点であるPvからy0Minが生まれた、という図です。
ここから連立方程式を立てましょう。
Pvを通る直線は、y=y0Min + a0*zで、Puを通る直線は、y=y1Max + a1*zです。
このyが等しくなる点なので、yを消去して、
y0Min + a0*z = y1Max + a1*z
zが入っているものを左に、それ以外を右に移すと、
(a0 - a1)*z = y1Max - y0Min
つまりzが解けて、
z = (y1Max - y0Min) / (a0 - a1)
となりました。zが出ればyも出るので、これでy,zが求まったことになります。
var z = (y1Max - y0Min) / (a0 - a1); var y = y0Min + (a0 * z);
Xはどうする?
さてYZ平面での計算は終わったんですが、 Xはどうしましょうか? 実は同じことをX軸についてもやります。
傾きを求める必要がありますが、a0、a1はさっき使って紛らわしいので、 ax0とax1としましょうか。さっきのa0、a1はay0、ay1と改名しましょう。
X軸、つまり画面の横方向は、縦に比べてアスペクト比倍の画角があります。
例えば縦画角が90度の時、その半分は45度ですから、傾きであるtan(θ/2)は1です。
画面が16:9で、横が16/9倍長い場合、この値に16/9を掛けるので、
傾きは16/9になります。
var ax0 = ay1 * camera.aspect; var ax1 = -ax0;
アスペクト比はCamera.aspect で取れます。16:9の横長なら約1.78、16:9の縦長なら約0.56が入っています。
これで同じように最小最大を求めていらない点を捨て、 xとzを同じように求めます。
求まったら、Y軸で求めたzと、X軸で求めたzを比べ、 小さい方を取ります。 もし、Y軸で求めたzが、X軸で求めたzより大きければ、 Y軸でやった時の方がカメラを前に出せる、ということです。 そうするとX軸では収まり切らないので、X軸を優先します。 小さい方、つまり手前を取るのはそういうことです。 そして、yとxはそのまま使います。それが中央だからです。
最後に、今求めたxyzはビュー座標系、つまりカメラのローカル座標での話なので、 これをワールド座標に戻して完成です。
以上からコード全体は、以下のようになります。
public Vector3 Focus(Vector3[] points) { // 全点をビュー空間に移動 var toView = Camera.transform.worldToLocalMatrix; for (int i = 0; i < points.Count; i++) { points[i] = toView.MultiplyPoint3x4(points[i])); } // 各種傾き var ay1 = Mathf.Tan(Camera.fieldOfView * 0.5f * Mathf.Deg2Rad); var ay0 = -ay1; var ax1 = ay1 * camera.aspect; var ax0 = -ax1; // XY軸で最小最大を取って不要データを捨てる var y0Min = float.MaxValue; var y1Max = -float.MaxValue; var x0Min = float.MaxValue; var x1Max = -float.MaxValue; for (int i = 0; i < points.Count; i++) { var p = points[i]; var by0 = p.y - (ay0 * p.z); var by1 = p.y - (ay1 * p.z); var bx0 = p.x - (ax0 * p.z); var bx1 = p.x - (ax1 * p.z); y0Min = Mathf.Min(y0Min, by0); y1Max = Mathf.Max(y1Max, by1); x0Min = Mathf.Min(x0Min, bx0); x1Max = Mathf.Max(x1Max, bx1); } // zを2つ求め、小さい方を採用する。x,yはそのまま使う var zy = (y1Max - y0Min) / (ay0 - ay1); var y = y0Min + (ay0 * zy); var zx = (x1Max - x0Min) / (ax0 - ax1); var x = x0Min + (ax0 * zx); var posInView = new Vector3(x, y, Mathf.Min(zy, zx)); // ワールドに戻す return Camera.transform.localToWorldMatrix.MultiplyPoint3x4(posInView); }
サンプルでの使い方
サンプルコードでは、CameraControllerというクラスのメソッドとして用意してあります。 インターフェイスは上とは若干異なり、もらった点の配列をそのままいじらず、 内部的に持っているテンポラリのListにコピーして計算しています。 できるだけ引数にもらったものは変更しない方が良いでしょう。
また、CameraControllerは補間の機能を持っており、 以前の記事 で紹介した指数関数補間を使っています。なので、ほどほど滑らかに動くわけです。
機能拡張について
収めたいものは点とは限りませんよね。 例えば球であったり箱であったりします。 しかし、いずれの場合も点の処理ができれば、それを利用して解くことができます。 球の場合は上下左右前後で6点くらい取れば実用上は十分ですし、 箱の場合は角の8点を生成すれば同じことになります。
また、「画面の外側10%は余裕を取りたい」 「画面下部と右側にはUIがあるので、それを除いた部分に入れたい」 といった要望もあるかと思いますが、これはわずかな改造で可能になります。 傾きを計算する所で、画面端の残したい領域を考慮するだけです。
終わりに
びっくりするくらい簡単でしたね。 何で思いつかなかったのかさっぱりわかりません。 球で近似して無駄に画面を余らせたり、 ビュー座標系での直方体で近似してやはり画面を余らせたり、 妙に無駄なことをしていました。
「向きを固定する」ということで何がどれだけ簡単になるかを把握できていなかったことと、 「最大最小はデータを捨てる手段である」という言語化、 視界端の平面を使って最小最大を取る値を作る、というあたりの思いつき、 などが何故か出てこなかったせいでしょうが、 なんとも不思議なものです。
