高さの影響を受けるフォグ 〜「低い所にガスが溜まってる」感を出す〜

unity shader math

画面写真をクリックするとWebGLビルドに飛びます。

こんにちは。技術部平山です。

今回は「高さ方向に変化があるフォグ」について扱います。 Unityに標準では入っていない奴で、 「地面付近に水蒸気が溜まってる感」とか「毒の沼地から怪しい霧が立ち登ってる感」 を出すのに使えます。京セラのS2(2014年のiPhone6plusの1/8くらいのGPU性能)でもまあまあ動きますので、 速度的な問題はあまりないでしょう。

ソースコードはgithubに置いてありますが、 残念ながら標準シェーダをコピーしてそこに追加してある、という形ではなく、 単にフォグだけやるシェーダを作っただけですから、すぐには使えません。 Fog.cginc にあるcalcFogHeightExp()を持っていって自分のシェーダに入れれば動くでしょう。 あるいは、作り方を学んでご自分で作っていただくとなお良いと思います。 バグっていない自信がありませんし、まだ高速化できることもわかっておりますので。

サンプルについて

WebGLビルドを用意したサンプルは、3つのフォグ手法の効果を比べるためのものです。 左側のExp,HeightUniform,HeightExp,Noneの4つの文字列はボタンになっており、 押すと切り換えられます。

  • Exp: 普通のフォグ。
  • HeightUniform: 高さが一定以上になると霧がなくなる
  • HeightExp: 高くなるほど徐々に霧が薄くなっていく
  • None: フォグなしです。

カメラはドラッグで回せます。 右端のスライダーは以下の通りです。

  • Strength : フォグ色が半分混ざる距離。高さで減衰する場合はy=0における設定。
  • Attenuation : 高さによって霧が薄まる度合い。
    • HeightUniform : この値の2倍の高さで急に霧が消えてなくなる。
    • HeightExp : 霧の濃さが半分になる距離。1とあれば、1m上がるごとに濃さが半分になる。
  • Cam Distance : (0,0,0)からのカメラ距離。引きで見たい時は増やしてください。

3つの手法について、頂点シェーダでやるか、フラグメントシェーダでやるかを選べます。 頂点シェーダの方が軽いですが、できる絵が変わってしまいます。 この例のように頂点が少ないと顕著に変わりますが、 それなりに頂点が細かければほとんど気づかれません。

f:id:hirasho0:20190813083211p:plainf:id:hirasho0:20190813083214p:plain

左がフラグメントシェーダ、右が頂点シェーダです。 HeightUniform設定なので、ある高さでくっきりと霧がなくなるはずですが、 頂点が少ないために、長く伸びた箱では上の方までフォグの影響が出てしまっています。 平坦な地面を4頂点で作ったりした場合にも問題になるでしょう。 頂点でやる場合は、ライティング上の必要がなくても頂点を多少は割っておく必要があります。

なお、画面下のスライダーは解像度でして、負荷測定用です。 右端にすると4096x4096で描画してベラボーに重くなりますので、ご注意ください。 私の京セラS2では2FPSくらいしか出なくなります。

速度について

結論から言えば、京セラS2ではほとんど負荷が見えません。 HeightExpが一番重くて、1510x1510の解像度で、 フォグなしに比べて1msくらいの追加負荷がありますが、 フォグなしでも47msかかっており、それが48msになるだけです。 そして、頂点単位にするとこの負荷が全く見えなくなります。

普通に3Dゲームができるような機械であれば、 ほぼ気にならないのではないでしょうか。 ただそれでも、一応頂点単位にすることくらいは試みておいて損はないかと思います。 そもそも「フォグなしで47msかかっている」がちょっと怪しいので、 もしかしたら何かの負荷に隠れて見えないだけかもしれません。 多少の用心は必要かと思います。

動機

つい先日、「立体的な霧を描きたい!!」という要望が出たのですが、 よく考えてみたらフォグについてはあまり真面目に考えたことがなかったことに気づきました。

今となっては、 volumetric lighting の一環としてフォグを表現する方が理論的に美しいと思うのですが、この手の手法は、

  • 3Dテクスチャを使う
  • シェーダの中でループ
  • ポストプロセスを使う

といった話になりがちです。しかし、我々の相手はスマホであり、 以前書いたように 性能には数十倍の開きがあります。 しかもフォグの類は画面の一部でなく全画面にかかるので問題になりやすいのです。 High Definition RenderPipelineには内蔵されている ようですが、LWRPすら重いわけで無理でしょう。

ですので、 「forwardレンダリングのシェーダにチョロっと足して、 負荷が増えたことに気づかないレベル」 でできる方法を探すことになります。 「for文書いたら負け」「if文書いたら負け」 という2005年頃の感覚で行きたいわけです(残念ながらif文は消せませんでしたが)。

一番簡単な奴をまず書いてみる

ややこしいのをやる前に、基礎になる簡単な奴を自作してみましょう。 「遠くなるほどフォグ色が混ざる」アレです。 Unityの標準シェーダに入ってるのでこれ自体を作る意味はありませんが、 私も理屈を忘れているので準備体操が必要です。

ところで、フォグを使って何をしたいのか、 というのは結構大事なので、作る前に整理しておきましょうか。

  • 遠近感を出したい
    • 遠くほど色が淡くなるのを表現することで遠近感が出るし、近くのものが背景から浮き彫りになる。
  • 霧や煙を表現したい
    • 風呂場とかもありますよね。パーティクル等と併用して雪や雨にも使えます。
  • 遠くの背景を出さずに済ませたい
    • 開発予算や処理速度から言って切実な事情ですが、晴れてるのに100mもない距離で急に真っ白になるのは嫌ですね。昔はよく見ましたが。

大きく分ければ、だいたい3つくらいでしょうか。 これら3つの用途にフォグが使える、ということは覚えておいて損はないと思います。 最後の理由はお客さんに直接言えるものではなく、言い訳として霧や煙を使うので、 表現としては同じになります。

そして、遠くで彩度が落ちるのと、霧や煙で視界が妨げられるのは、違う現象に思えますが、 「遠くほど元の色が見えにくくなる」という意味では同じです。 だからフォグという一つの仕掛けで表現できるわけです。

物理的に考える

「遠くに行くほど、物の色を霧の色で置き換える」 ということをすれば、フォグが実現できます。 「どれくらい遠くで」「どれくらい色を置き換えるか」は匙加減であり、 無限の方法がありうるでしょう。 それはアートの問題であって、良いアートになるように仕掛けを作れば良いと言えます。

しかし、アートとは別に、現実世界がどうなっているのかを知っておくのは 悪くないと思います。 現実世界はみんな見慣れているので自然に見えます。 リアルを求めるなら現実と同じ仕掛けにした方がリアルですし、 リアルを求めないにしても、良い出発点になるはずです。

物体の色は、その色の光として視点にやってきます。 その過程で、空気中にある何かがその光を邪魔してしまいます。 吸収するのかもしれませんし、跳ね返すのかもしれませんが、 それはまあ考えないことにしましょう。

空気中に漂っている塵や水滴その他にぶつかるのは確率的な現象ですので、 例えば1m進む度に10%の確率で光がぶつかって邪魔されてしまう、 としましょう。光の粒が10個とかしかなければ、 1個だけ失われる確率が一番高いでしょうが、一個も失われなかったり、 2個失われたりすることもあります。 しかし光の粒はムチャクチャたくさんあるので、 「ピッタリ10%失われる」としても問題ありません。 これも中心極限定理ですね。

  • 1m進むと光が10%失われて90%になります。
  • さらに1m進むとさらに10%失われて、81%になります。
  • さらに1m進むとさらに10%失われて、72.9%になります。

だいたいこんな調子です。ではこれを式にしましょう。

color -= color * 0.1;

1m進む度にこの処理をします。しかし、 シェーダの中でこれを馬鹿正直にやるのはちと重いですね。 1km先なら1000回回さないといけません。 そこで、ちょっと変形します。

10%引くのは、90%になるのと同じなので、 0.9を掛けましょう。そしてそれを繰り返すならば累乗が使えます。

color = color * pow((1.0 - 0.1), distance);

distanceに5が入っていれば5乗です。 4.5などの中途半端な値なら、まあいい具合に間の値になるでしょう(雑!)。

distanceは、頂点シェーダでワールド座標を計算してフラグメントシェーダに渡し、 カメラの座標と引き算して求めます。

struct v2f{
    float3 worldPosition : TEXCOORD2;
    float4 vertex : SV_POSITION;
};

v2f vert (appdata v){
    v2f o;
    o.vertex = UnityObjectToClipPos(v.vertex);
    o.worldPosition = mul(unity_ObjectToWorld, v.vertex);
    return o;
}

fixed4 frag (v2f i) : SV_Target{
    float distance = length(i.worldPosition - _WorldSpaceCameraPos);

unity_ObjectToWorldをmulすればワールド座標が得られ、これをフラグメントシェーダに渡し、 _WorldSpaceCameraPosがカメラの座標なので、引き算してlengthすればいいわけです (組み込みの変数一覧は公式にあります)。

元の色がRGB(1, 0.5, 0)で、2m先にあるのであれば、 0.9を2乗して0.81ですから、RGBは(0.81, 0.405, 0)となります。

f:id:hirasho0:20190813083155p:plain

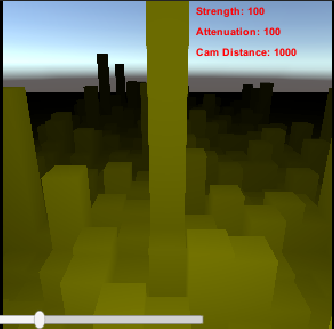
だいたいこんな感じになります。 このシェーダもサンプルに入れてあります。 元の色は黄色でして、それが遠いほど暗くなっていきます。 って、あれ?暗くしたいんじゃないですよね?

暗くしたいんじゃない

遠くほど光が減っていけば、当然暗くなります。 でも、やりたいのはそうじゃないですよね?霧だったら白くなるでしょうし、 遠くの景色なら灰色になっていくでしょう。 つまり、そういった別の色を足す仕掛けが必要です。

実は、物から来た光がはじき飛ばされて失われるのと同じように、 他のどこかではじき飛ばされた光が視点に飛び込んでくることもあるのです。 ですから、暗くなる一方なわけではないわけですね。

真面目に考えると「どこでどの色の光がはじき飛ばされて、こっちにやってきたのか?」 なんてことも気になりますが、そんなのとても計算できないので、 「はじき飛ばされて消えた分だけ、好きな色の光を足しちゃえ!」 とお気楽に考えましょう。 外の風景なら白でしょうし、毒の沼地なら紫でしょうか。

というわけで、「失われた量」が必要です。

color = color * pow((1.0 - 0.1), distance);

のpow((1 - 0.1), distance)が、減った後の量ですから、 これを1から引けば出ますね。

var lost = 1.0 - pow((1.0 - 0.1), distance);

そして、この分だけ、テキトーな色を足します。 マテリアルにプロパティーを足して設定してもいいですが、 標準の仕組みでフォグの色を設定しているはずなので、それを使いましょう。

color = color * (1.0 - lost);
color += unity_FogColor * lost;

何もしなくてもunity_FogColorという変数がシェーダで使えるようになっているので、 それを使います。

線形補間の利用

ところで、

(x * a) + (y * (1 - a))

の形の計算は線形補間(Linear intERPolation: LERP) と呼ばれていまして、シェーダでは専用命令が用意されています。 そっちの方が短く書けるので(速いとは断言できない)使いましょうか。

color = lerp(color, unity_FogColor, lost);

引数の順番に気をつけましょう。 lostが大きいほど増えるのはunity_FogColorで、 それを後ろに持っていきます。 まあ間違っても「近くほどフォグ色になる」 というわかりやすい状態になるのですぐ気づきますけどね。

さあ、これが基本のフォグのシェーダ、ということになります。 コード全体はこちらにあります。

f:id:hirasho0:20190813083159p:plain

powを消す

さて、今のコードにはpowという命令があります。

これは実は複合命令でして、unityはこの命令を分解したコードを生成します。 手動で分解しておくことで、高速化できるかもしれないわけです。

また、powは微積分との相性がよろしくありません。

pow(x, a)

をxで微分したい、と思ったらどうすればいいでしょうか?

指数関数の微分で基本になるのは、exの微分です。コードっぽくexp(x)と書きましょうか。 exp(x)は微分してもexp(x)のままという素晴らしい性質があるので、 微分積分の気配がする時には、累乗や対数は全部底を自然対数eにしてしまう方がいいのです。 そうしてexpに慣れてくると、「とりあえず全部それで良くね?」という気分になって、 powを見ると全部expにしたくなってきます。

というわけで、expにしましょう。

pow(a, b) = exp(log(a)*b)

です。この公式を覚えていればいいんですが、 毎日数学めいた仕事をしているわけでもなく、たまに使う程度では公式を思い出しても不安しかないので、 その都度導出することをおすすめします。

a^b           # 対数を取ろう
log(a^b)      # logの中にある累乗はlogの外に出して掛け算にできる。bを外に出そう。
log(a)*b      # さっき対数を取ったので戻そう
exp(log(a)*b)

という具合です。「logの中にある累乗はlogの外に出して掛け算にできる」だけ覚えておけば、 毎度導出した方が安心感があります。

というわけで、

var lost = 1.0 - pow((1.0 - _Attenuation), distance);

を、

var lost = 1.0 - exp(log(1.0 - _Attenuation) * distance);

に変換できました。あとは、 log(1.0 - _Attenuation)をC#側で計算してからMaterialに入れてくれれば いいわけです。ちなみにこれがどれくらいかと言うと、 例えば_Attenuationが0.1の時には、log(0.9)で、-0.1053...といった感じになります。 「1より小さいもののlogはマイナス」というのが感覚としてわかると、 絵に絡む仕事をするのに便利かと思います。

なお、この-0.1053...をlog(1-0.1)で計算して求めるのでなく、 直接指定できるようにしてしまってもいいかもしれません。 「1mにつきどれくらい失われる」のような意味はなくなりますが、 どうせスライダーで設定するのであれば、単位を気にする人なんてまずいません。 その場合もマイナスは邪魔なので、プラスで指定させて、 シェーダでマイナスだけ処理します。シェーダでは符号反転はタダだからです。 それに、log(1-x)はだいたい-xと近い数になります。今も0.1053と0.1で ほとんど違いませんよね(テイラー展開して1次で打ち切ってみましょう)。

これを_Strengthという名前にすると(大きいほどフォグが強くなるので)、

var lost = 1.0 - exp(-_Strength * distance);

となり、コードはシンプルになります。

lerpをひっくり返して1からの引き算を消す

さて、lostを求めるのに1.0から引き算しているのですが、 実はこれはナシにできます。

lerp(a, b, x) = lerp(b, a, 1-x)

なわけです。順番を入れ換えたら、補間率を1から引いて、ひっくり返します。

var a = exp(-_Strength, distance);
color = lerp(unity_FogColor, color, a);

1.0から引くのをやめて、名前をaにしました(いい名前が思いつかない)。 そして、lerpの引数をひっくり返しました。 コードが短くなって良いですね。 実行速度も速くなるかもしれませんが、 コンパイラが賢ければこれくらいはやってくれているかもしれません。

高さの影響を受ける

では次の段階として、高さの影響を受けるようにしましょう。

高くなるほど、つまりYが大きくなるほど、霧が弱くなるわけですが、 その方法は無限にあります。 まずは簡単な奴を試しましょう。

一定高度で霧がなくなる、とします。例えばこんな感じです。

f:id:hirasho0:20190813083203p:plain

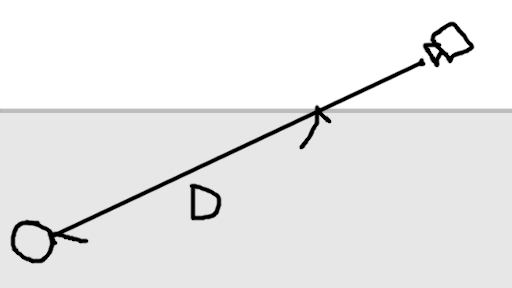
カメラが霧の上にいて、モノが霧の中にあります。 図中でDとある長さが、 「どれくらい霧の中を光が移動してくるか」です。 これを、上のコードのdistanceと置き換えれば計算完了となります。

ではDはどうやって求めるか?結構簡単です。

f:id:hirasho0:20190813083205p:plain

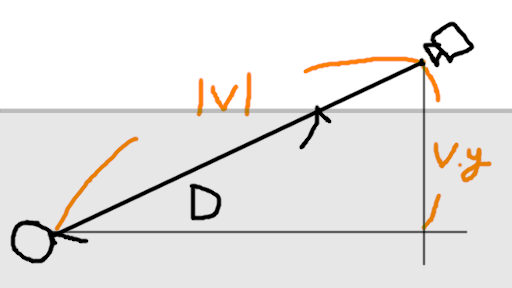
カメラからモノまでの距離はすでに求まっています。図中には、 「カメラからモノへのベクトルをv」としたかのように書いてあります。 その長さ|v|と、そのy成分v.yがわかれば相似で求まりますね。 霧の上端のy座標をh、モノの座標をpとした時、

|v| / v.y = D / (h - p.y)

です。Dについて解けば、

D = |v| * (h - p.y) / v.y

となります。これをdistanceと取り換えて終わりです。

場合分けが...

でも、実はそう簡単ではなかったりします。 今は「カメラが霧の外にいて、物が霧の中にある」ケースですが、 パターンはこれだけではありません。

  • カメラが霧の外にいて、物も霧の外にいるケース
    • 霧がかからない。D=0。
  • カメラが霧の外にいて、物が霧の中にいるケース
    • さっきやった。
  • カメラが霧の中にいて、物が霧の外にいるケース
    • さっきと違う式になる。
  • カメラが霧の中にいて、物も霧の中にいるケース
    • 全体が霧の中なので、カメラと物の距離がそのままD。

この4つの計算は共通化できないので、ifで分岐するしかなくなります。 サンプルではこうなっています。

float calcFogHeightUniform(float3 objectPosition, float3 cameraPosition, float fogDensity, float fogEndHeight)
{
    float3 v = cameraPosition - objectPosition;
    float t;
    if (objectPosition.y < fogEndHeight) // 物が霧の中にある
    {
        if (cameraPosition.y > fogEndHeight) // カメラは霧の外にある
        {
            t = (fogEndHeight - objectPosition.y) / v.y;
        }
        else // カメラも霧の中にある
        {
            t = 1.0;
        }
    }
    else // 物が霧の外にいる
    {
        if (cameraPosition.y < fogEndHeight) // カメラは霧の中にいる
        {
            t = (cameraPosition.y - fogEndHeight) / v.y;
        }
        else // カメラも霧の外にいる
        {
            t = 0.0;
        }
    }
    float distance = length(v) * t;
    float fog = exp(-fogDensity * distance);
    return fog;
}

endFogHeightが霧の上端です。コードの整理のために0から1の範囲になるtを求めて、 それにカメラと物の距離を掛けることで霧の中に入る長さを求めています。

結果はこんな感じです。

f:id:hirasho0:20190813083211p:plain

ある高さから下だけ紫になっているのがわかりますね。 2mから上は霧がない、という設定です。 急に霧がなくなるのが不自然ではありますが、 用途によってはこの方が合うことはあるかもしれません。

ただ、汎用と考えるとイマイチです。なだらかに薄くなっていく方が いろんな状況で使えます。

ところで、if文は重い、というイメージがあるのですが、 今回はその重さが全く見えませんでした。 S2のGPU(adreno)のプログラミングガイド には、「ピクセルごとに別の経路を通り得る分岐は重い」と書かれているので、 「やらないに越したことはない」という程度には思っておいた方がいいとは思います。

高くなるほどだんだん薄くなる

さて、最初にこんなコードを出しました。

color -= color * 0.1;

1メートル進む度に10%づつ削られていく時の、 「10%削る」を表現したコードです。

今度は、この「10%」が高さによって変化します。

color -= color * calcFogDensity(y);

みたいな感じですね。0.1を「霧の濃さ」と解釈して、 この0.1を求める関数をcalcFogDensityとしておきました。 それに今いる点の高さyを渡す感じになります。 しかし、このままで実行しようとすると、 ループが必要になります。 濃さが一定でないので「ループを累乗にして高速化」ができないのです。

for (...)
{
    color -= color * calcFogDensity(y);
}

とループで引いていく行為は、つまるところ積分です。 積分した式が前もって求まれば、ループなしで計算ができます。 というよりも、ループなしでやれるようにするために、 綺麗に積分できる式を作ろう、という話になるのです。

なお、ここから先の内容は下町のナポレオン-フォグの実装 では数学記号を使ってエレガントに解説されていますので、 数学記号が大丈夫な方はそちらをおすすめします。

積分できる関数を作る

さて、積分しやすい関数と言えば、x^2+2x+4のような多項式か、 e^xのような指数関数です。特に指数関数は最高で、 積分しても微分しても形が変わらないので非常に楽です。 また今回の場合、「高さがどんな値でもプラスのままでいてくれる」 という性質がないと、霧の濃さがマイナスになって厄介です。 さらに「高くなるほど薄くなる(=単調減少)」が保証されている必要もあります。 これらの条件を考えると多項式は使えません。

というわけで、「霧の濃さは指数関数的に変化する」としましょう。 今、霧の濃さd(densityの略)が、

d = d0 * exp(-k*y)

で表せるとしましょう。d0が、y=0の時の霧の濃さです。 そして、kは何かのパラメータで、これが大きいほど、速く霧が薄くなります。 expの中身がマイナスであれば、expの結果は0から1の間になり、 k*yが大きいほど結果は0に近づきます。薄くなるわけです。

さて、1m進む度に色が失われていくのは、

color -= color * calcFogDensity(y);

という具合に書いていました。これから積分をするので数学に寄せた記法で書けば、 1ステップは、

dc/ds = -c * d0 * exp(-k*y)

という感じになります。sで微分、としていますが、このsというのは、 「光が進む方向の距離」です。距離が100なのであれば、 カメラの所で0、物の所で100になるような変数sがあるとします。 このsについて、0から100まで積分すればいいわけです。 colorはcとして、1ステップごとの変化量dc/dsは、 今の色cに、その高さの霧の濃度を掛けたものだ、ということになります。

まずyが邪魔

今sで積分しようとしているわけですが、右辺にyがいます。 yは「その時点での高さ」で、sが変わればもちろん変化します。 なので、yをsで表しましょう。

y = y0 + (v.y / |v| * s)

です。物の高さをy0、 カメラから物へのベクトルがvで、 |v|はその長さ、v.yはそのy成分です。 sが|v|と同じになれば、分子分母が消えてv.yが残り、 これをy0に足せばカメラの高さになります。 間は線形補間です。

dc/ds = -c * d0 * exp(-k*(y0 + (v.y / |v| * s)))

めでたくsだけの関数になりました。「え、これ積分すんの?」 って感じですね。でも幸いにしてできます。

まず、式を単純化しましょう。まず、expの中がややこしすぎるので、 二つに割ります。

exp(a+b) = exp(a) * exp(b)

を使います。10の(2+3)=5乗は10万だが、それは10の2乗=100に、10の3乗=1000を掛けたものと同じ、 という話です。

dc/ds = -c * d0 * exp(-k * y0) * exp(-k * v.y / |v| * s)

ここで、

A = d0 * exp(-k * y0)
B = -k * v.y / |v|

としてしまいましょう。こいつらは定数です。

dc/ds = -c * A * exp(B * s)

だいぶマシになりました。さて、右辺にcとsで二つ変数がいて邪魔ですね。 こんな時は変数分離と言って、cを左辺に、sを右辺に寄せます。

dc / c = -A * exp(B * s) * ds

dc/dsで一つの記号なのに、こうやって割っていい理由を 私はまだ人に説明できるほど理解していません。 でも、「すごく小さいcを、すごく小さいsで割ったものが、dc/ds」 と雑に解釈するのであれば、dsを両辺に掛けたって良さそうに思えます。 実際いいみたいです。

さて、分離できたので、左辺をcで、右辺をsで積分します。 なんでそうしていいのかは、やはり説明できるほど理解していません。

左辺は1/cの積分でして、これはlog|c|になります。 右辺は指数関数の積分でして、exp(ax)を積分するとexp(ax)/a になることを利用します。積の微分 を積分に応用すれば出てくるので、自力で導出するのも簡単です。以上から、

log|c| = -A/B * exp(B * s) + 積分定数

となります。不定積分ができました。欲しいのはlog|c|じゃなくてcなので、 両辺expに入れてlogを外したいのですが、 式が長くなる前に定積分を求めちゃいましょう。

sに|v|を入れたものから、sに0を入れたものを引きます。

-A/B * (exp(B * |v|) - exp(B * 0))

Bは-k * v.y / |v|でしたから、sが|v|になると約分できますね。 さらにexp(0)は1ですから、右半分も簡単になって、

-A/B * (exp(-k * v.y) - 1)

これで求まったのはcの対数log|c|なので、expでくくって、

|c| = exp(-A/B * (exp(-k * v.y) - 1))

今はプラスだけ相手にすればいいので、cについた絶対値はそのまま外しちゃいましょう。 さらに、A,Bを元に戻します。

c = exp(d0 * |v| / (k * v.y) * exp(-k * y0) * (exp(-k * v.y) - 1))

かくして、積分したものが求まりました。expが二重になってて大丈夫なのか? 感がありますが、 ここまで来たらとりあえず実装して、絵がそれっぽくなればオーケーです。

float calcFogHeightExp(float3 objectPosition, float3 cameraPosition, float densityY0, float densityAttenuation)
{
    float3 v = cameraPosition - objectPosition;
    float l = length(v);
    float ret;
    float tmp = l * densityY0 * exp(-densityAttenuation * objectPosition.y);
    if (v.y == 0.0) // 単純な均一フォグ
    {
        ret = exp(-tmp);
    }
    else
    {
        float kvy = densityAttenuation * v.y;
        ret = exp(tmp / kvy * (exp(-kvy) - 1.0));
    }
    return ret;
}

ifで分岐してますね。これは何かと言うと、視線が水平、つまりカメラと物の高さが同じだった場合です。 先程の説明で言うv.yが0だと、0除算が発生してしまうので、正常に計算できないのです。

実のところ、数学的には不要な分岐でして、

(exp(ax) - 1)/a

はaが0でも正常に計算できます。expのテイラー展開は

exp(ax) = 1 + ax + (ax)^2/2 + ...

なので、ここから1を引いてしまえば、残りの項は全部aで割れるからです。 ですが、シェーダでテイラー展開を計算する余裕はありませんので、 組み込みのexpを使ってしまって、ダメな時だけ分岐、とせざるを得なかったりします。

なお、「そのピクセルにおける物のy座標がカメラと完全一致することなんてまずない!」 と割り切ってしまうこともでき、その場合は分岐を消せます。 万が一完全に一致したとしても、その画素の計算がおかしくなるだけのことです。 たぶん黒くなります。稀に画面に黒い点が出るくらいなら気にしない、という選択肢はアリです。 速度を測って気になるくらい遅かったら私もそうすると思います。 しかし上で述べたように大して遅くなかったので、とりあえずこのままにしてしまいました。

終わりに

後半の積分で、私はノートを4ページ消費しました。 本当、私は数学向いてないと思います。

そして、これくらい数学臭が強くなってくると、コード風に書くのはもう限界かなという気もしてきますね。 普通に積分の記号を出せよ、という気がしてきます。 皆さんはいかがでしょうか。数学記号使って大丈夫な方はこんな記事いらないと思うんですけどね。

なお、この「高さが上がるほどexpで薄くなるフォグ」は CryEngineで採用されていたそうです。 すでに実績のあるやり方なのであれば、ちょっと安心ですね。

おまけ: パラメータを与えやすくする

サンプルでは、霧の濃さを「フォグ色が50%混ざる距離」として与えるようにしています。 300にすれば、300m先のもので灰色になる、といったイメージです。 物理的な根拠のある数字を入れられるので、うれしい人はうれしいでしょう。 でも大半の人は理屈ガン無視でただスライダーをいじって決めると思いますので、 そうする意義があるかどうかは微妙ではあります。

ただ何にせよ、デシベルの時にお話したように、 スライダーは対数化しておきましょう。 0.0001とか0.001とかを対数でないスライダーで入れるのは不可能です。 まして、意味のわからない値をテキストボックスで直打ちさせるのはなおさら論外だと思いますので、 必ずスライダーは用意すべきだと思います。

おまけ: 実はもっと速くできる

今回のシェーダには多数のexp()がありますが、 Unityでexp()と書くと、コンパイラが別の形に変換してしまいます。

exp2(a * log2(e))

と展開されてしまい、命令の数が増えてしまうのです。ちょっとコンパイルされたシェーダを覗いてみましょうか。

u_xlat0.x = u_xlat0.x * _FogStrength;
u_xlat0.x = u_xlat0.x * 1.44269502;
u_xlat0.x = exp2(u_xlat0.x);

元々exp(k*_FogStrength)と書いてあった箇所が、3行に割れてしまいました。 1.4426..というのが、log2(e)です。 本気で高速化したいのであれば、シェーダをexp2を使う形に直す必要があります。 マテリアルに定数を設定する段階で1.4426..倍しておけ、ということですね。

ただ、今回は測定しても遅くなかったし、面倒くさいのでそこまではやっていません。 特に「高さによって霧が薄くなる奴」では、積分の関係で単純に定数を1.4426..倍しただけでは 動かないので、結構面倒くさくなります。その価値はないかもしれません。

おまけ: 本筋に関係ないこと少し

サンプルの箱の高さは、先日紹介した対数正規分布 で作っています。大半のビルは似たような高さだが、たまにベラボーに高いビルがある、 というようなことをしたかったのです。

もう一つ、サンプルではライトマップを利用しています。 極力軽い処理で物の形が見えるようにしたかったからです。 自作のシェーダでライトマップを貼る際のサンプルとしては、 フォグなしのシェーダ が短くて便利かと思います。 【Unite Tokyo 2018】カスタムシェーダーでモバイルでも最先端グラフィックスな格闘ゲームを！ を参考にいたしました。ありがとうございます。