動画をクリックするとWebGLビルドに飛びます。 今回のサンプルコードもgithubに置いておきましたが 、あまり役には立たないと思います。
こんにちは。技術部平山です。
今回は軽いお話です。 対数正規分布 をご紹介します。
動機
前回の記事では、 ランダムにドラッグしたり長押しさせたりするために、 ドラッグする距離と、長押しする時間を乱数で決めていました。
もしここでフツーにRandom.Range()を使うとどうなるでしょうか。
var distance = Random.Range(0f, 1000f); var duration = Random.Range(0f, 3f);
こんな感じでしょうか。距離は1000ピクセルまで、時間は3秒まで、 という感じです。しかし、普通操作のほとんどはドラッグではなくタップですよね? 上記コードでは押している時間の平均値は1.5秒ですが、 タップで1.5秒ってことはまずありません。それは長押しです。 ドラッグの距離も、平均は500ピクセルで、これも完全にドラッグです。 こうなると、タップの時とドラッグや長押しの時は分岐して別物にして しまわないと話になりません。ほとんどがドラッグや長押しになってしまうからです。
しかし、タップであっても押して離すまでの時間はバラついてほしいですし、 押して離す時にちょっとズレたりもしますよね。 だからタップであっても乱数は欲しいところです。 どうせどちらも乱数を使うなら、一つにしたいとは思いませんか?
他にも、キャラの能力値をバラつかせる、というような時にも
同じような要望が出るかもしれません。
ヒットポイントは80点から120点、という時に、
Random.Range(80f, 120f)とすると、120点や80点のキャラが100点のキャラと同じくらい
出てしまいます。例えばモンスターを味方にするゲームで、
微妙にモンスターの能力に個体差がある、みたいな時に、
120点の確率は落として100点付近に集めたい、と思ったりするかもしれません。
さて、このRandom.Rangeで出てくるような
どこでも同じ感じに出る乱数を一様分布といいます。
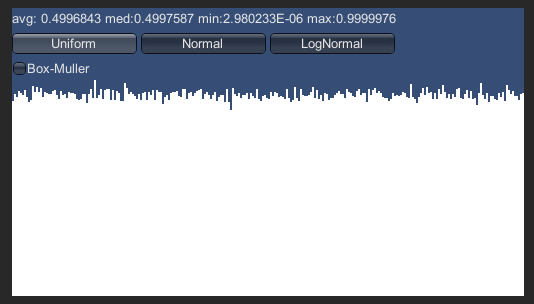
これは一様分布のヒストグラムを描いてみたものです。乱数なので デコボコはありますが、上から下までほぼ一定の頻度なのがわかります。
正規分布
普通にRandom.Rangeを使うと、最大値付近も、平均値付近も、同じくらいの 確率になってしまいます。しかし、少なくともタップ距離、タップ時間の例では、 平均値は最大値よりずっと小さくしたいですし、 平均値付近が良く出て、最大値は滅多に出ない、としたいわけです。 そこで分布をいじりましょう。
分布の世界で一番メジャーなのは、何と言っても正規分布 です。平均値付近がたくさん出て、外れるほど確率が下がっていきます。 それでいて、ものすごく外れた値であっても確率がゼロになりません。
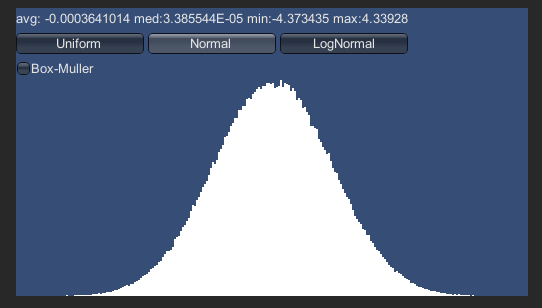
グラフを見ると、多くは真ん中に集まっていて、中央から外れるほど急激に確率が下がっていきます。 この例では、平均値、つまり真ん中はほぼ0で、ほとんどが-2から2の間に ありますが、最大値は4.3となっています。かなり離れたものもたまに出る、ということです。
コードで正規表現を作る
正規分布をプログラムで生成するには、近似で良ければこんな感じにします。
float NormalDistribution() { var ret = 0f; for (int i = 0; i < 12; i++) { ret += Random.value; } return ret - 6f; }
0から1の乱数(Random.value)を12回足し、6を引いて平均を0にすると、 ほぼほぼ正規分布になります。サイコロをたくさん振って足せば正規分布を近似できますが、 これはその例です。 バラつき具合はテキトーな値を掛けて調整し、望みの平均値を足してズラします。 今の例なら、
var distance = Mathf.Abs(NormalDistribution() * 333f); var duration = Mathf.Abs(NormalDistribution() * 1f);
とかしてみましょうか。マイナスはいらないので絶対値を取りました。 一番多いのはゼロ付近だろうということで、何も足さずに使っています。
上の関数で出てくる正規分布は標準偏差が丁度1なので -1から1に入る確率がだいたい7割くらいです。 そして、-3から3に入らない確率が0.3%くらいあります。 なので、333倍すれば、標準偏差が333になるので、 -1000から1000に入らない確率が0.3%くらいになり、 そのへんが最大値かな、という気分になります。 時間の方は長くて3秒、大抵は0秒付近、ということで悪くない感じです。
偏差値
学校にいた時代にさんざん気にした偏差値という奴は、 学生の点数が正規分布すると仮定した時に、 どれくらい平均から外れているかを表す値です。 平均を50とし、標準偏差分外れる度に10足したり引いたりします。 偏差値70は、標準偏差2個分外れているということなので、 この例で言えば、666ピクセルの距離は偏差値70、ということになります。 東大行けそうな印象ですよね。666ピクセルはなかなか出ないんだろう、 という気がしてきます。
また、モンスターの能力値の例で言えば、
var hp = Mathf.Abs(NormalDistribution() * 10f) + 100f;
とすれば、100点なら偏差値50、110点で60、120点で70、となります。 120点はなかなか出ないでしょうし、130点が出たら宝物って感じですね。
先程のグラフでは、最大値が4.3でした。標準偏差1の分布ですから、 偏差値は90ということになります。サンプル数は50万ですから、 50万人もいれば偏差値90が一人くらいはいるかもね、 という雰囲気だということですね。 もちろん現実の学力は完全に正規分布というわけではないのですが。
まだ平均がデカい
さて、モンスターはこれでもいいかもしれませんが、 タップの件はまだ不満です。30%の確率で333ピクセル以上の距離になってしまう、 ということは、「ほぼほぼドラッグになってしまう」ということです。 もっと極端に、小さい値の確率を上げ、大きい値の確率を下げたいのですが、 このままでは難しいものがあります。例えば、
var distance = Mathf.Abs(NormalDistribution() * 5f);
とすれば、10ピクセル以下にほとんどが集中しますが、 こうなると1000ピクセルの距離は絶望的に出なくなります。 標準偏差の4倍以上離れる確率は15000分の1くらいです。 偏差値90は1万人に1人もいないということです。 そして5倍ともなれば200万分の1くらいで、もう出ません。偏差値100ですから。 標準偏差5で1000ピクセルというのは標準偏差の200倍ですから、 宇宙が終わっても出ないくらいの確率になります。
別の分布が必要ですね。
対数正規分布
さあ、ここで対数正規分布です。 簡単に言えば、正規分布で出てきた値で、何かを累乗します。
var x = Mathf.Pow(10f, NormalDistribution());
「正規分布を累乗するのに何故対数?」と思うかもしれませんが、逆です。 「対数を取ると正規分布」の意味ですね。対数「が」正規分布、 と「が」を補うとわかりやすいでしょう。
さて、ここでは感覚がつかみ易いように10を累乗しています。
NormalDistribution()が0を返せば、
10の0乗で1、1を返せば10、2を返せば100になります。
3以上を返す確率は0.15%くらいですから、0.15%くらいの確率で1000ピクセルになり、
98%の確率で100ピクセル以内、
85%の確率で10ピクセル以内、となります。
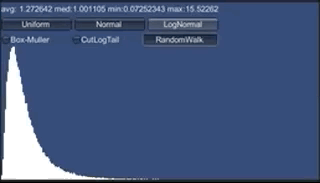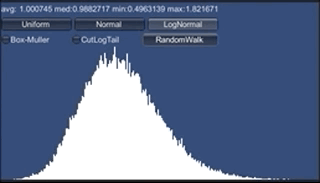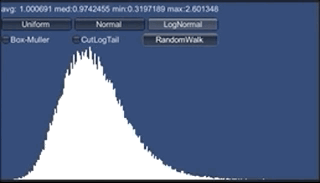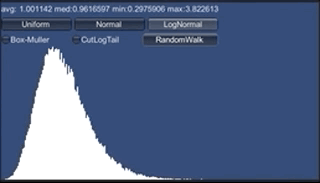
対数正規分布のグラフはこんな感じです。
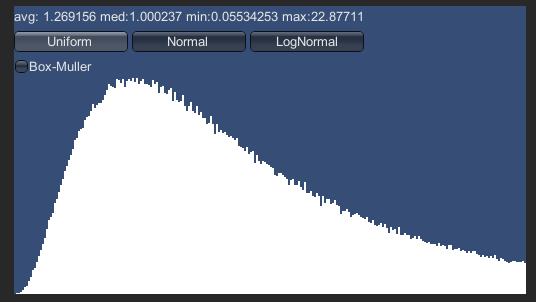
おおよそ下の方に集まっていて、上の方はどこまで伸びるかわからない感じです。
最大値まで入るようにグラフを描くとこうなります。
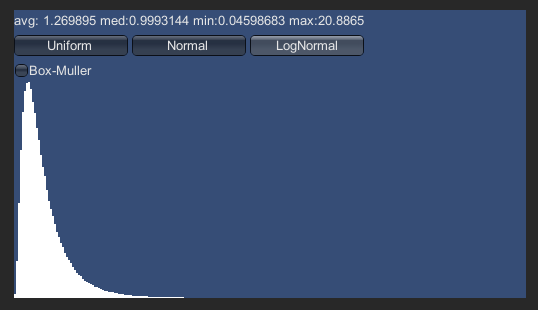
数が少なすぎて見えませんが、右端にもデータがあるのです。 ほとんどは下の方に集まっています。 画面の上の方に統計量が出ていて、平均値が1.2なのに最大値が20を超えています。
「ほとんど小さくていいが、たまに突出してデカいのが欲しい」 という要望に合っていますね!
なお、NormalDistribution()がマイナスを返しても問題はなく、
-1なら10の-1乗=1/10で0.1、-2なら0.01、
と限りなく小さくなっていきます。
完全に0にはなりませんが、ほぼ「0が最小値」と考えて良いでしょう。
ドラッグ距離やタップ時間にマイナスは不要ですので、絶対値を取るまでもなく0以上になる
この性質は便利です。
そういうわけで、前の記事で出てきた自動タップのサンプルでは、 この分布を使ってドラッグ距離とタップ時間を決めているわけです。 もっといい分布はあるでしょうが、「とりあえず」としては上出来でしょう。
対数正規分布が使える局面
対数正規分布でググれば わかりますが、この分布はお金が絡む問題で良く出てきます。
- ある時点でみんな1万円持っている
- 1年ごとにそれぞれの人は何%か減ったり増えたりする
という状態で放っておくと、だいたい対数正規分布になります。 プラスx%のxに大きい値が連続した人は複利でお金が増えていって すごいことになり、普通の人の何倍何十倍というお金になります。
試しに、ずっと10%だった人とずっと1%だった人を比べてみましょうか。
- 10%で40年 → 45倍
- 1%で40年 → 1.5倍
30倍の差がついてしまいました。「資産運用は大事ですよ!定期預金で寝かせてない?」 って台詞をよく聞きますが、まさにこれです(まあ今時10%はないですが、 2%確保するか0.1%で放っておくかでも結構差はつきます)。
プログラムでシミュレーションしたのが以下です(RandomWalkボタンを押します)。
最初はみんな同じ額なんですが、どんどん差が開いていきます。 グラフは勝手に拡大縮小されるのでわかりにくいのですが、maxを見ていれば 上の方はどんどんお金が増えてすごいことになっていくのがわかるはずです。
実際に、国民の年収をグラフにすると だいたいこんな感じでして、少数の大金持ちはすごいことになっている状況がよくわかります。
ドラッカー という人は「社会現象は正規分布でなく対数正規分布する」 というような(正確な物言いは違う)ことを本に書いていて、 実際お金のような「人間が絡んだ現象」に多く見られます。 「ツイートのリツイート数」「ゲームの売り上げ」「芸能人のファン数」 なども似た感じでしょう。ごく少数の上位者がケタ外れの値を持ちます。
「2位じゃダメなんですか?」という台詞が批判されたのは、 社会が対数正規分布に従うからでしょう。 1位と2位では何倍も収益が違ってしまうのです。 ゲームなどのコンテンツ商売は「収益が対数正規分布」つまり「2位じゃダメ」 という恐怖と戦わねばならないわけで、まったくもって恐ろしいですね。 なお、自然現象でも「油田の規模」のように対数正規分布っぽいものが 多数あります。「上位の油田の埋蔵量だけで大半を占めてしまう」 ということで、デカい奴をたまたま見つけるとすごいことになるわけです。
平均値と中央値
対数正規分布している時の平均値は、 感覚的な平均値、つまり「多くの人がこれくらいの値」という値からは かなり外れます。少数の超お金持ちが平均を引っぱり上げてしまうからです。
会社のデータで平均年収が出てたりしますが、あれ、大抵信用ならないですよね? これは年収が対数正規分布していて、平均が上にズレているからかもしれません。 「ゲームの平均売り上げはいくらですごい」と言っても、 ほとんどは赤字で、数個のビッグタイトルが利益を独占しているのです。
そういう現象で「一番ありがちな値」を知るには、 中央値を取る必要があります。 今回のサンプルでもこのことが現れていて、

画面上部に平均(avg)と中央値(med)があるのですが、 それぞれ1.27、1.00とかなりズレています。 その原因は、10とか20とかを叩き出しているごく少数のサンプルです。 この例では最大値は22.8で、フツーの人(=中央値)の20倍を超えています。 まったくもって社会の縮図ですね。
この場合は27%のズレですから、 年収で言えば、平均は381万だけど、中央値、つまり 一番ありそうな感じの人は300万でした、というような話になります。 実際年収にはそれくらいの開きがあって、 先程リンクを貼った年収の統計 でも中央値が記載されていますね。平均値547万に対して中央値427万ですから、 だいたい同じ感じのズレです(10年前の統計なので今の中央値はもっと低そうですが)。
ゲームでの応用
さて、これをゲームで使える局面は他にあるでしょうか?
基本、「社会の縮図」的な要素があるゲームであれば、 予測やテストデータの生成に使えます。 ソーシャルゲームでダミーのユーザデータを作る場合、 やり込み度、つまりはゲーム内リソースの量をこの分布に従って設定すれば、 それっぽい感じになるのではないかと思います。 理屈で考えても、上で示したように「一定時間ごとにランダムに何%か増えるものがたくさんある」 的な要素があれば対数正規分布なわけで、 「レベルが高いほど経験値がたくさんもらえる」的な構造を考えれば、 ある時間ゲームをした時の増え方は掛け算的になるはずです。 予測も簡単ですし、テストデータも作りやすくなります。
同様に、ゲームの中に擬似的な経済がある場合、資産の分布はだいたい 対数正規分布になると予測できそうです。
また、「社会の縮図」感がなくても、 「小さいのがたくさんあって、たまにすごいデカい」が欲しければ まずこれを試すのがいいでしょう。 対数正規分布に近い現象である必要はありません。 人のドラッグ距離やタップ時間は対数正規分布からは程遠いでしょうが、 それでもそれっぽい値を作るのには役に立ちます。
あとは、デバッグ時にネットワークの通信待ち時間をシミュレーションする際には、 待ち時間を対数正規分布にすると良いと思います。 「大抵はすぐAPI返ってくるけど、たまにすごい待たされる」 という現実によくある状況を簡単な式で表現できます。
おわりに
今日のは技術の話というよりは、与太話ですね。
しかし、分布を意識して現象を見るとゲームで表現する時にも違ってくると思いますし、 日常生活でも便利です。 私が思うに、素人でも使えて大事な分布は、一様分布、正規分布、そして対数正規分布の三つです。 何かがバラついている時に、どの分布に似たバラつき方なのか、 を考えると、対処がしやすく、プログラムで表現したり予測したりすることもしやすくなります。 特に正規分布は「標準偏差1個分の間に70%、2個分の間に95%、4個分はまず超えない」 ということを感覚で把握しておくと、利用価値がぐっと上がります。 偏差値で考えるとわかりやすい、と言うことならそれも良いでしょう。 こんな便利なものを学力にしか使わないのはもったいないことです。
また、一様分布を足しまくると正規分布、というのも重要な知識です。 中央極限定理 ですね。 サイコロを繰り返し振るとか、毎フレーム同じ量だけランダムに移動する、 とかいう場合の挙動は正規分布になるわけです。 最初全部1にして、ランダムな値毎フレーム足していった場合のグラフはこうなります。
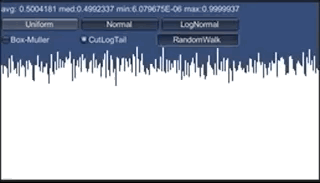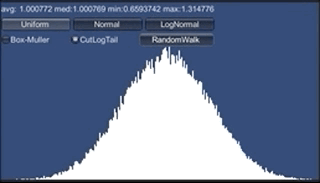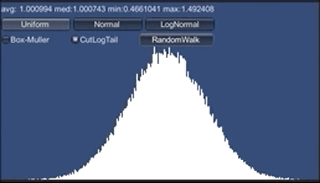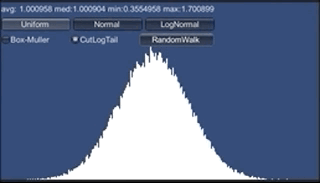
あっというまに正規分布になりますね。
正規分布ですから、上で見たように「中心から外れると急速に確率が減る」つまり「だいたい真ん中に寄る」 ということになります。ランダムにパーティクルを動かした際の挙動、などはだいたい想像がつくことになります。
また、これを拡大解釈して「多少尖っていてもいずれ丸くなる」と思っても 間違いではないでしょう。うちの娘は幼児の頃は背が突出して高かったのですが、あっさり平均値になってしまいました。 身長は正規分布に従うことが知られています。
その一方で、対数正規分布に従う現象であれば、突出したものは桁外れに突出しますから、 その「桁外れ」になるべく努力を重ねるのもいいでしょう。何かの分野で一番になれば、 能力では二番と大差なくても、全然違う名声やお金を手にできるかもしれませんよ。
おまけ: 正規分布を真面目に求める方法
ボックス=ミュラー法 を使えば近似でなく正規分布を求められます。乱数を12回呼ぶよりも速度も良いでしょう。 今回はこれと近似を選べるようにしてあります。コードはこんな感じです。
float normalDistributionCosine = float.MaxValue; // MaxValueが入ってる時は計算が必要。 float GetNormalDistributionBoxMuller() { float ret; if (normalDistributionCosine != float.MaxValue) // 前に作った奴が残っていれば返す { ret = normalDistributionCosine; normalDistributionCosine = float.MaxValue; } else { var x = Random.value; var y = Random.value; var t0 = Mathf.Sqrt(-2f * Mathf.Log(x)); var t1 = Mathf.PI * 2f * y; normalDistributionCosine = t0 * Mathf.Cos(t1); ret = t0 * Mathf.Sin(t1); } return ret; }
一回の計算で2個出てくるのが特徴であり、使いにくい点でもありますが、 速度がどうでも良ければ片方を捨ててしまっても大丈夫な気はします。捨てる場合は、 毎回計算してCosかSinのどちらかを返せばいいでしょう。
おまけ: 01乱数を12回足したら標準偏差1の正規分布っぽくなる理由
0から1の乱数を12回足して、6を引く、というのは、 6を12個の乱数に分配すると、 -0.5から0.5までの乱数を12個足すことに相当します。
標準偏差というのは分散の平方根です。分散というのは、 「出た値から平均を引いたものの二乗、の合計」ですね。 「-0.5から0.5の乱数」の平均は0ですから、 出た値をそのまま二乗すれば分散です。
さて、この乱数の分散の平均値はいくつでしょうか。 それには、分散を-0.5から0.5まで積分すればわかります。
x^2を積分するとx^3/3ですね。xに0.5を入れると1/24で、-0.5を入れると-1/24なので、
引いて1/12となります。積分の幅が0.5-(-0.5)=1なので、このままこれが平均値です。
1個あたり分散が1/12で、12個足すと分散も12倍になって1になります。標準偏差はその平方根なので、1です。めでたい!
このことは奥村先生のサイト で読んで知り、ちょっと感動しました。「12個足したらいい感じ」ということ自体は 調べれば頻繁に出てくるのですが、私の数学力では根拠がわからなかったのです。 でも上のように、ちゃんと考えればわかる理屈で、 考えることを放棄していたことを恥ずかしく思います。
おまけ: ダメージが正規分布
昔、ウィザードリィ というゲームがありました。 このゲーム、ダメージがサイコロで決定されるので、バラつきがすごいのです。
例えば攻撃一回あたりサイコロ1個という武器があるとします。 1から6の一様分布ですね。これじゃ全然予測が立ちません。 弱いうちは攻撃回数が少ないので毎回がバクチで、運が悪いと一瞬で殺されます。
しかしゲームが進んでくると攻撃回数が増えて、正規分布に近づきます。 1から6であっても、8回攻撃なら平均は28、サイコロの分散は1個あたり35/12で、8倍して280/12、 平方根を取って標準偏差にすると4.8。つまり、まあまあ18-38くらいに収まるだろうと 予測が立つようになります。安定こそ強さですね。 まあゲームが進むにつれて一撃死する確率が上がってきて、やはり気を抜けば死ぬのですが。 年とともに腕が上がって安定するのと並行して、育児や健康などで謎の負荷がかかって気が抜けなくなるのと似ています。 ゲームは人生の縮図です。
このように、分布のデザインによってゲームデザインに特徴を与えることもできるかと思います。 ウィザードリィ以外にそんなにバラつくゲームは知りませんが、 ドラクエでもバギ系はやけにバラつくということがありました。 いっそダメージを対数正規分布にしたらどうなるんでしょうね?
確率や分布の知識はゲームデザインにも役に立つと思いますし、 プログラマとして参加していても、デバグやツール作り、さらにはAI作りなどに役立つことと思います。