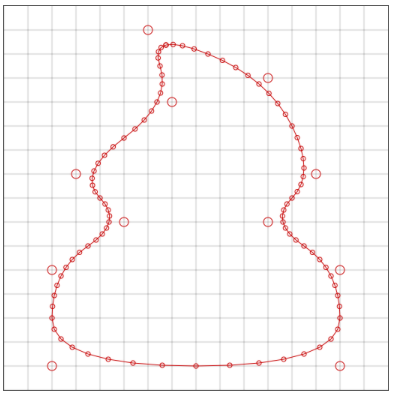
画面写真をクリックするとサンプルアプリに飛びます。 今回はサンプルがhtml5ですので、それがそのままソースコードですが、 一応githubにも置いてあります。 内部に「ここからここまでライブラリ」的なコメントがあるので 、その部分だけ持っていけばライブラリとして使えます。
こんにちは。技術部平山です。
今日は、B-スプライン曲線を使って点を補間し、 曲線を生成する方法について書きます。いくつかの説明記事を読んでもさっぱり理解できず、 結局は自分で説明を考えることになりました。せっかくだからブログにしようと思った次第です。
動機
つい最近ゲームを試作している時に、曲線を生成したい状況になりました。 アーティストさんにモデリングしてもらえばいいのですが、 曲線の形状がゲーム性に直結するため、 先にゲームデザイン作業の一環として曲線を生成してゲームを検証し、 それが済んでからモデリングをお願いしたいな、と思ったわけです。
最終的にはUnityのEdgeColider2D に渡して当たり判定に用いるので、データは短い直線の集合である必要がありますが、 手でたくさん点を打って曲線っぽいものを作るのはあまりにも面倒なので、 大まかに何点か打つと勝手に曲線を作ってくれる機能が何としても必要です。
「そんなのベクタ系の描画ソフトを使えばいいのでは?」 と思われるかもしれませんが、今回は、 以前の記事でご紹介した ように、スマホ実機にブラウザからアクセスして形状を編集し、 即座にゲームに反映したいのです。 他のゲーム要素の配置も同じツールで行いますから、 別ツールを併用するのは面倒くさすぎます。 今回のコードがjavascriptなのはそういう事情によります。
よくある補間3種類
さて、点を何個か打つといい具合に曲線を生成してくれる、 という用途に使えそうなメジャーな技法は3つあります。
それぞれ特徴があります。粗く書くと、
- ベジエ
- N点用意するとN-1次式で近似してくれる。端点以外は通らない。
- スプライン
- 全部の点を通るように複数の3次式(とは限らないが普通3次)を生成する。
- B-スプライン
- どの点も通るとは限らない、複数の2次式(とは限らないが)を生成する。
まずベジエは合いません。点が10個あれば9次式になってしまい、 次数が高い曲線は計算も大変ですし、波打ってあんまり綺麗にならない印象があります。 何点かづつ区切ってベジエ化することも考えられますが、 ちょっと面倒くさそうです(できるのかもしれません)。
次にスプラインですが、「全部の点を通る」が今回の用途では合いません。 例えば「4点打ったら、その内側に収まる丸っこい図形を生成したい」 というような用途だからです。

点を通ると、外側にはみ出した図形ができるため、 それを考慮に入れて点を打たないといけなくなります。 また、計算が結構面倒くさい(連立方程式が出てくる)という欠点もあります。
そして最後のB-スプラインですが、 これは2次式という「曲線になる最も低い次数」で生成できて計算が楽そうな上に、 打った点からはみ出さないという性質もあり、理想的に思えました。 実際うまく行きました。
しかし、残念ながら理屈がよくわからないのです。 そこで、自分にもわかる説明を考えてみることにしました。以下でそれを述べます。
「点を混ぜて線を作る」という考え方
点が何個かあった時に、それをつなぐ方法はいろいろあります。 一番簡単なのは、線形補間です。
隣合う2個の点のブレンド率を変えていくと、 2点の間の点が得られ、それをつなげると線になります。
ここで、
- 混ぜる点の数は2点である。
- ブレンド率の合計は1である。
ということに注目します。 2点のブレンド率の合計が1から外れると、 2点を結ぶ線分の外側の点ができてしまいます。 だから、ブレンド率の合計は絶対に1です。
そして、今は2点しか混ぜていないので、 2点を含む直線から外れた点はできません。
さて、ではこれを拡張して曲線を作るにはどうしたらいいでしょう?
3点に増やす
ブレンドする点の数を増やしましょう。
3点を、ブレンド率の合計が1になるように混ぜると、 3点が成す三角形の内側のどこかの点ができます。

隣り合う3点を、ブレンド率の合計が1になるように混ぜながら、 少しづつ後ろの点のブレンド率が高くなるようにしていけば、 だんだんと進んでいって線ができるはずです。 そして、どこかのタイミングで使う3点を一つずらして、 違う三角形に移れれば、点がたくさんあっても一つの曲線になりそうに思えます。
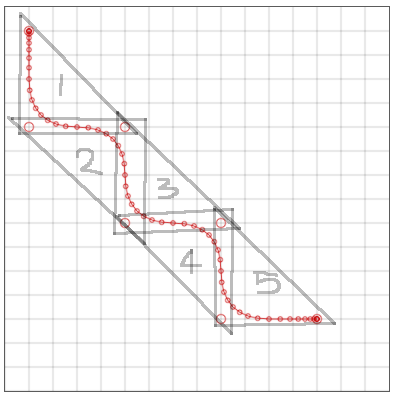
図には7個の点があり、隣合う3個から5つの三角形ができます。 それぞれの三角形でブレンド率の合計を1に保ちながら 三角形を渡り歩いていくわけです。
ブレンド率を変える関数
さて、こうなると問題になるのは「どうやってブレンド率を変えていくか」です。 まずは簡単な線形補間でブレンド率がどうなるのか見てみましょう。
最初は0番が1、1番が0です。そうすると0番頂点と同じ点になります。 だんだん0番を減らし、1番をその分増やし、いずれ1番が1になり、 0番の寄与が0になります。 ここで、線を切り換えますね。0と1からでなく、1と2で線を作るように 変えるわけです。この後は、1番の寄与が減っていき、2番の寄与が増えていきます。
グラフにするとこんな感じです。横軸は点の番号(0,1,2,3...)、 縦軸はブレンド率です。

左端の方にある緑の線が、0番のブレンド率です。 これが下がるのと同時に、青の1番のブレンド率が上がってきます。 上がり切ったら、次は黄色の2番のブレンド率が上がってきて、 青い1番は下がっていきます。 なお、それぞれの山のてっぺんの高さにある水平な黒い線は、合計です。 方眼の1マスは0.25なので、4マス分の高さの所に黒い線があることは、 合計が1であることを示しています。 それぞれのブレンド関数の山の幅は2です(方眼8個分)。
さて、これと似たようなことを3点でやりましょう。 満たす条件は以下です。
- それぞれの山の幅は3
- どの場所でも3つの山が重なっていて、高さの合計が1
線形補間の時と同じような単純な三角山では、これは実現できません。

とりあえず幅を1.5倍に広げてみたものですが、合計(黒い線)が1になりません。 もっと凝った形の何かが必要らしい、ということがわかります。
二次関数の導入
そこで、二次関数を使ってみましょう。 二次関数で山を作るには、2次の項の係数をマイナスにすればいいですね。 ただ、単純に幅が3の二次関数を並べても合計が1になるはずはないので、 上に凸の二次関数を上下ひっくり返して下に凸にしたものをつなぎます。 幅3の中央1を上に凸、両端の1を下に凸にするわけです。 この山の形が滑らかでなければ、 それを使ってできる曲線も滑らかにならず折れてしまうでしょうから、 うまいこと折れないように係数を調整してつなぎます。 そして、合計が1になるように全体の大きさを調整すると、

このようになりました。合計を表す黒い線が直線になり、 めでたく一定になりました。 それぞれの山は幅が3なこともわかります。
実際、これを使って隣り合う3点を混ぜていくと、 2次のB-Spline曲線ができます。 この混ぜ具合を計算する関数は以下のような感じです。
var calculateBasisWeight2 = function (basisT, t) { var ret = 0; var nt; if (t < (basisT - 1.5)) { // 何もしない } else if (t < (basisT - 0.5)) { nt = (t - (basisT - 1.5)); ret = 0.5 * nt * nt; } else if (t < (basisT + 0.5)) { nt = (t - basisT); ret = 0.75 - (nt * nt); } else if (t < (basisT + 1.5)) { nt = (t - (basisT + 1.5)); ret = 0.5 * nt * nt; } return ret; };
basisTというのが「何番目の点の混ぜ具合か」で、
tは0番の点がいる場所を0、1番の点がいる場所を1、
とした時の座標です。0.1なら0番から1番へ向かう途中の10%地点、
ということになります。時刻と考えてもわかりやすいでしょう。
「0番を0時に通り、1番を1時に通り...」という具合です。
3区間に分割されていて、両端では2次の項の係数がプラスで下に凸、 中央ではマイナスなので上に凸になっていることがわかります。
曲線を描く時には、このtを0からちょっとづつ(例えば0.01づつ) 増やしながら、混ぜる点の番号3つを渡して上の関数を呼んで ブレンド率を求め、点を混ぜるわけです。
あるtにおいて、混ぜる3点の番号は簡単に求まります。
例えばtが2.4なら、山の幅は3なので、その半分の1.5を引いて、
0.9ができます。0番の点は含まれませんから、その次からですね。
つまり、ceil(t - 1.5)が最初の番号です。そこから3つを
混ぜればいい、とわかります。
他の説明と全然違う気がする
さて、ここまでは、他のサイトの説明を英語含めて 5個以上読んだのにさっぱりわからなかった私が考えた説明です。 数学的な厳密さは全くありません。
普通B-Splineといえばノットベクトルとかいうものが出てきて、 再帰的なアルゴリズムで基底関数とやらを作るはずです。 iやjやkが混ざったややこしい式を実装しないといけないのでは?
実は今回の実装と説明はB-Splineの特殊なケースだけを扱っています。 だから単純なのです。
- ある点が一番たくさん混ざる時刻、的なパラメータtを「点の番号と同じ」としてしまっている。
- ノットベクトルを調整できないので、「この区間は長い」みたいなことが表現できない。
- 2次しか扱わない。
- 3次以上のブレンド関数(他では基底関数と呼んでいる)は手動で作るのは骨。
- 他のサイトにあるちゃんとした式なら何次でも作れる。
しかし、一旦これでイメージを掴んでからの方が、 汎用的な手法の説明を読んでも頭に入りやすいと思います。 「3個の点を幅3のブレンド関数で混ぜ合わせるのが2次のB-Splineなんでしょ」 と考えれば、話は簡単で、難しい式も出てきませんし、とりあえずは使えます。
ただ、それはあくまで単純化した話であって、 例えば今回「幅が3」なのは、「k番の点が一番混ざる時刻がt=k」 としたことによります。1番をt=2、2番をt=5、 といった具合に設定することもできて、 そうなれば幅は違ってくるのです。 必要であれば、より一般的な理論を理解した方が良いでしょう。 残念ながら平山は数学が苦手なので、 必要が出てくるまではここで止めておきます。
端の処理
2次のB-Splineでは「常に3点を混ぜる」ので、
1点、あるいは2点だけを混ぜて点を作ることはできません。
ブレンド関数の合計が1にならないと、おかしな所に行ってしまうからです。
最初の点をt=0とする場合、tが1.5を超えないと、
2番の点のブレンド関数の範囲に入らず、3つのブレンド関数を用意できません。
つまり、t<1.5の領域では点を作れないのです。
そこで、今回の実装では、-1番や-2番の点をでっちあげ、 そこでもブレンド関数を計算するようにしています。
でっちあげる方法としては以下の2つが選べます。
- 0番より前は全部0番
- 0番の1個前は最後の点とする。つまりループする。
前者の場合、t=0だと混ぜる3点が全部0番になるので、 つまりt=0で0番そのものになります。0番の点から始まるわけです。
後者の場合、最後の点に向かって補間されるので、輪になります。
同じ処理は末尾でもやっていて、点の個数をNとする時、
- N-1番より後は全部N-1番
- N-1番の次は0番
のいずれかを選べます。サンプルでは「ループ」というチェックボックスとして
用意してあります。
コードはそう難しくもありません。cyclicで検索して出てきた所がそれです。
おわりに
いや本当数学は難しいですね。半日いろんな説明を読んで、 さっぱりピンと来なかった時の絶望感といったらもう。
最初は理解してからコードにしようと思うわけですが、 あまりにわからないので、書いてある式をそのまんまコードにしてみるわけです。 まあ、動くには動くわけですね。確かに。
でも、iとかjとかkとかが入り乱れて、しばらくはバグってましたし、 「端では曲線を作れない」ということに気づくのがずいぶんと遅れて悩んだり、 「ループさせたいんだけどどうしたらいいの?」となったりして、 本当さんざんでした。
さて、これで形状を作れるようになったので、 ここから計算でメッシュを生成して、それをアセット化する、 というところに取りかかる予定です。 仮にアーティストさんにモデリングしてもらうにしても、 寸法図を渡すよりは、メッシュのアセットを渡した方が良いでしょう。
そのあたりも、そのうちブログにすると思います。
参考文献
- 日本語wikipedia
- 実装に必要な情報は揃っているが、理屈はさっぱりわからない。
- 英語wikipedia
- 日本語よりかなり詳しいが、よくわからない。Definitionの所では添字が1始まりで、下のPropertiesでは0始まりなのはなんで?とかそういうレベルでわからない。
- Tajima Robotics
- かなりわかりやすく、実装に必要な情報も揃っている。
- 武蔵システム
- 幾何的なイメージが掴みやすい。しかし「少なくとも一つはオンカーブ点が含まれます」の意味がよくわからなかった。サンプルで示したように、一つも点を通らないB-Splineは生成できる。
- 緑川章一の個人ページ
- ブレンド関数を作る方法の最大のヒントになった。
- MITのサイト
- たぶん一番ちゃんとした説明だと思う。図はイメージを掴む助けになった。
いずれのサイトも、「ノットベクトルってどこから出てきたの?」 「端の処理はどうしたらいいの?」 という疑問にダイレクトには答えてくれなかったのですが、 たぶん私が読み取れなかっただけだと思います。
この記事の著者・平山のインタビュー
この記事の著者・平山のインタビューをカヤックサイトで公開しています。ぜひご覧ください!