補間関数で作るアニメーション

プログラムで動きを作ることは結構あります。

操作せずに観賞するアニメーションであれば、 アーティストが作る方がいい出来になると思うのですが、

• 操作によって介入があるアニメーション
• 場所や大きさ、速度、数などがゲームの状況に応じて変化するアニメーション
• アーティストが作るまでもないアニメーション

のようなものはプログラマがやることが多いかと思います。 この記事では、技術部平山 がコードでアニメーションを作る際の基礎知識について書いてみます。

なお、少々数学臭が強くなりました。平山は正直数学が苦手でして、 かなり苦労して書いております。間違いがありましたら連絡頂ければすぐに修正いたします。 さらに、「時間を取って平山に数学を教えてやろう」 という方がいらっしゃいましたら、泣いて喜びますので、よろしくおねがいいたします。

とりあえず見てみてください

動きの話は文章で説明しても辛いので、まずは見ていただこうと思います。 実行可能なサンプルをweb上に置いておきました。 こちらを実行しながら見ていただけると良いかと思います。

「Linear」から始まるボタンの行に関数の名前が並んでいるので、 適当に選んで押してください。下の行にあるrewindボタンを押すと最初の位置から再生されます。 最初の位置と最後の位置が決まっていてその間をつなぐのですが、 つなぎ方が関数によって変わります。 たくさんキーフレームを置いていい感じのアニメを作る、 という路線はアーティストにお任せし、ここでは「計算で間をつなぐ」ことだけを考えています。

また、右下のグラフは拡大率を毎フレームプロットしたもので、 動きの性質がなんとなくわかります。

コードをいじりながら見たい方、ローカルで動かしたい方は、 githubにサンプルコード を置いておいたので、そちらをご利用ください。

では、関数それぞれを見ていきましょう。

線形補間(Linearボタン)

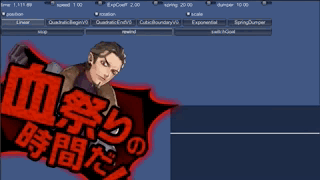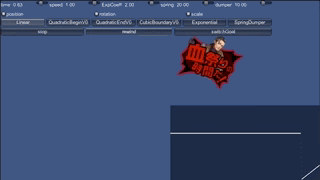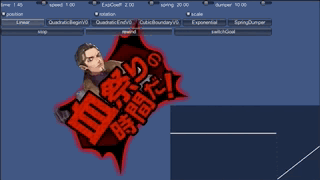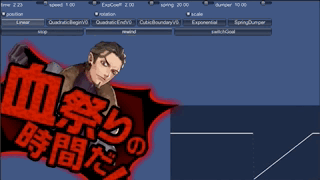
最初の値と最後の値を直線的につなぎます。 例えば角度なら、最初が0度で2秒後に180度なのであれば、1秒後は90度です。

実装は簡単です。まず、今の時刻が、最初の値を取る時刻と、最後の値を取る時刻の 間のどのへんにあるかを求めます。

例えば、時刻1で90度、時刻3で180度、今の時刻は2、 ということであれば、1と3の真ん中なので0.5とします。 0.5は50%の意味で、「時刻1の値と、時刻3の値を50%づつ混ぜる」ということになります。

では、この0.5はどう計算するか。こうです (サンプル内の相当するコード)。

t = (now - t0) / (t1 - t0);

t0は最初の時刻(ここでは1)で、t1は最後の時刻(ここでは3)です。 今の時刻である2から、1を引きます。これを、二つの時刻の差で割ります。 そうすれば0から1になるわけです。 あとは、このtがブレンド率になっているので、ブレンド計算を行います。

p = (p0 * (1f - t)) + (p1 * t);

最初の値をp0、最後の値をp1としました。 tが0なら最初の値であるp0に、tが1なら最後の値であるp1になってほしいので、 p0には1-tを掛け、p1にはtを掛け、それらを足します。

なお、この式だと演算子が、掛ける、引く、足す、掛ける、で4つあり、 ちょっと無駄が多いので、大抵は以下のように変形します (サンプル内の相当するコード)。

p = ((p1 - p0) * t) + p0;

p1からp0を引いたものに0から1であるtを掛け、それにv0を足すわけです。 UnityEngine.Mathf.Lerpの中身はこれです。 ここで、a=(p1-p0)、b=p0と置くと、p=at+bという一次関数であることがわかります。

さて、こいつの動きはいかがでしょうか。 素直と言えば素直ですが、面白味はありません。 私は0.2秒以内で終わるものでない限り、これで動きをつけることはあまりしません。 ちょっと手抜き感があります。少なくとも、生き物はあまりこういう動きをしません。

二次関数補間、初速ゼロ(QuadraticBeginV0ボタン)

では、線形補間以外にどんな形が考えられるでしょうか。 「線形」というのはp=at+bのような「一次関数」のことですから、 次は二次関数にでもしてみましょう。p=at^2+bt+cです。

式の形を決める値がa,b,cで3つあります。 最初の値と最後の値で式が2つできますが、 未知数は3個あるので式が足りません。 何かしら式を追加して連立方程式を解くことになります。

連立方程式

「連立方程式なんて言葉は何年ぶりかな」という方も いらっしゃるかもしれないので、 先程の一次関数を題材に連立方程式を解いてみましょう。

今関数の形をp=at+bと置きます。aとbを知りたいので、 未知数は2つです。 最初の時刻0と最後の時刻1で取るべき条件から、

p0 = a*0 + b
p1 = a*1 + b

と式が2つできます。1つ目から即座にb=p0がわかり、 これを2つ目に代入すればa=p1-p0が出てきます。 つまりp=(p1-p0)t+p0が求まります。

では二次関数も同じやり方でやりましょう。 まず、式2つは最初の値と最後の値から決まります。

p0 = a*0*0 + b*0 + c
p1 = a*1*1 + b*1 + c

式が足りないので、何らかの条件を足すのですが、 ここでは「開始時の速度(初速)が0」としてみましょう。

速度というのは、関数の微分のことです。 p=at^2+bt+cを微分すればp'=2at+bになります。 これが、時刻0で0なので、

0 = 2*a*0 + b

となり、式が3つ決まりました。0や1を消して整理して並べると、

p0 = c
p1 = a + b + c
0 = b

となります。bとcはすでに求まっていますね。 1,3つ目を2つめに代入すればaが求まり、

a = p1 - p0
b = 0
c = p0

となります。関数形はp=(p1-p0)t^2+p0となりました。 計算するコードは、

float a = p1 - p0;
return (a * t * t) + p0;

となります (サンプル内の相当するコード)。

動き

さて、こいつの動きはどうでしょうか。サンプルのQuadraticBeginV0です。

速度ゼロから徐々に加速してくる感じはいいのですが、 唐突に止まるあたりに少々不自然さを感じます。 現実世界で急に止まるのは衝突した時で、 若干行き過ぎたり、変形したり、反発したりするものです。 それがないのが物足りないのでしょうか。 終わった所でエフェクトや音による「衝突感」があれば いいのかもしれません。

式について補足

できた関数はp=(p1-p0)t^2+p0ですが、これはt^2をsと書くと、 p=(p1-p0)s+p0となり形が一次関数と同じになります。 ということは、tを二乗してから一次関数に放り込めば同じ結果になるということです。 一次関数による線形補間で書いた後で「加速が欲しいな」と思ったら、

t *= t;

と一行書くだけで二次関数になり、加速感が出ます。

二次関数補間、終速ゼロ(QuadraticEndV0ボタン)

初速ゼロがあるなら、終わりの速度がゼロ、というのも考えられます。

動き始めが鋭いので、ボタンを押した時の反応などには良さそうです。

そういえば、「人間は、原因から結果までの間が0.14秒以上空くと、因果関係を感じられなくなる」 とどこかで読みました。本当かどうかは知りませんが、 私はそれを聞いてからというもの、押したら0.14秒以内に十分大きな 反応が出るように作ることを心がけています。 例えばポップアップなどは0.14秒以内に十分広がるようにしています (サンプルの「popup motion」というトグルを押すと、アニメーションが ポップアップ風に変わるようにしておきました)。

求める

では関数の形を定めましょう。

2つの時刻での値から式が2つ、というところは同じで、 速度、つまり微分の条件で式を1つ作る所も同じです。 ただ、速度条件が「時刻1」についてのものになります。

0 = 2*a*1 + b

ちょっと変形するとb=-2aとなり、b=0よりは解くのが面倒ですね。 解くと、

a = p0 - p1
b = -2 * (p0 - p1)
c = p0

となります。計算するコードは素直に書けば、

var a = p0 - p1;
var b = -2f * a;
return (a * t * t) + (b * t) + p0;

ですが、こうやって書くと、かけ算が多くて遅いし、誤差も大きいしで、いいことがありません。 p=at^2+bt+cを、できるだけtでくくって、p=(at+b)t+cと変形し、 これをコードにします。

var a = p0 - p1;
var b = -2f * a;
var ret = a;
ret *= t;
ret += b;
ret *= t;
ret += p0;
return ret;

atを計算し、bを足し、それにtを掛け、cを足します (サンプル内の相当するコード)。 見やすいように演算一個ごとに1行使いましたが、return (((a*t) + b) * t) + p0;とくっつけてもいいでしょう。 こうやって多項式を計算する方法をホーナー(horner)法 と言います。

三次関数補間、初速ゼロ、終速ゼロ(CubicBoundaryV0ボタン)

二次関数の場合、初速か終速のどちらか与えられません。 未知数が3個なので、式が3つしか立てられないからです。 もし、始まりも終わりも速度ゼロにしたければ、 関数をもっと複雑にして未知数を増やす必要があります。 そこで、三次関数にしてみましょう。

求める

関数形はp=at^3+bt^2+ct+dとします。 まず、時刻0と1での値がp0,p1なので式が2つできます。

p0 = a*0*0*0 + b*0*0 + c*0 + d = d
p1 = a*1*1*1 + b*1*1 + c*1 + d = a + b + c + d

いきなりdは解けました。次に、速度の条件で式を2つ立てます。 微分はp'=3at^2+2bt+cなので、

0 = 3a*0*0 + 2b*0 + c = c
0 = 3a*1*1 + 2b*1 + c = 3a + 2b + c

となります。cも解けました。未知数が2個に減ったので式を整理してみましょう。

p1 = a + b + p0
0 = 3a + 2b

1つ目をb=...に直して2つ目に代入するのが楽ですかね。解くと、

a = 2(p0-p1)
b = 3(p1-p0)
c = 0
d = p0

となり、計算するコードは、hornor法で、

float a = 2f * (p0 - p1);
float b = 3f * (p1 - p0);
var ret = a;
ret *= t;
ret += b;
ret *= t;
// c=0なので何も足さない
ret *= t;
ret += p0;
return ret;

となります (サンプル内の相当するコード)。

動き

動きはこんな感じです。

始まりから加速して、減速して終わります。滑らかさが欲しい時には便利そうです。

操作と相性がいい補間が欲しい

さて、4つほど見てきましたが、この4つには共通点があります。 「時刻が決まると値がビシッと決まる」ということです。 必要な変数が時刻だけなので扱いが楽な一方、実は困ることもあります。

ポップアップ開けてる最中に閉じたい問題

今、ボタンを押すとポップアップが拡大しながら出てくるとしましょう。 関数型は何でもいいのですが、「終わり速度0の二次関数」 あたりが良いでしょうか。 さて、そのポップアップが完全に拡大し切る前に、 再度ボタンが押されたとします。 こういう時は、おそらくキャンセルでしょう。 ポップアップを閉じます。

いきなりパッと消してもいいと言えばいいのですが、 もし閉じる時にもアニメーションをつけたい、ということになると少々面倒です。

まず、同じ関数を逆に辿って消すなら簡単なのですが、 操作に対する反応は鋭い方がいいと思います。 終わり速度0の二次関数は減速で、逆に辿ると加速になりますから、 それでは反応が鈍いのです。

そこで、「開ける時と閉じる時で別の関数を用意する」 ということがやりたくなります。 開ける時も閉じる時も「終わり速度0の二次関数」を用意するのですが、 開ける時は「スケール0から1へ」、閉じる時は「スケール1から0へ」となり、 値が違いますから、これは違う関数です。

そして、例えばt=0.8で閉じるボタンが押された場合、 閉じる関数のそれに相当するtを計算して、そこからアニメーションを開始します。

具体例で説明しましょう。

開ける時には、t=0でスケール0、t=1でスケール1となる、終わり速度0の二次関数を用意します。 関数はp=-t^2+2tです。 閉じる時には、t=0でスケール1、t=1でスケール0となる、終わり速度0の二次関数を用意します。 関数はp=1-t^2です。

今ボタンを押して、ポップアップを出しました。アニメーションが進行し、 t=0.5でもう一度ボタンを押し、そこから閉じるとします。 t=0.5の時にはp=-(0.5*0.5)+(2*0.5)=0.75です。75%の拡大率になっています。 これを閉じる方の式であるp=1-t^2にあてはめます。

p=1-t^2=0.75なので、t=の形に解いて、t=sqrt(0.25)で、t=0.5とt=-0.5の 二つの解が出てきます。今の場合マイナスの解は無視できますから、プラスを取りましょう。 t=0.5から閉じる方のアニメーションを再生するわけです。

さて、今は関数型が単純だからまだ良かったのですが、もうちょっと複雑になると、 この作業がひどく面倒くさくなります。両方とも三次だったらどうなるか考えてみてください。 p=at^3+bt^2+ct+dの関数で、今pが0.8だったとします。相当するtはいくつでしょうか? これは3次方程式を解く問題で、結構面倒ですし、しかも答えが一つとは限りません。

というわけで、「途中で何か横槍が入って、別の関数につなぎたい」 というような場合には、もっと楽な方法が欲しくなるのです。

逐次計算で表現する

途中で横槍が入ることを前提とするならば、 「今の値」を持っておいて、そこに毎フレーム修正を加えて動かしていくのが簡単でしょう。

例えばポップアップの例で言えば、 まずスケール0から始めて、毎フレーム0.1を足していけば、10フレームで1になります。 もし途中でもう一度押されたら、今度は毎フレーム0.1を引いていけば、そのうち0になります。 面倒な計算はいりません。

p += 0.1 * Time.deltaTime;

実際には上のように、Time.deltaTimeを0.1に掛けてから足します。 でないと、フレームレートが高い機械ほど速く動いてしまうからです。

実に簡単なのですが、残念ながらこれは線形補間と同じ動きで、あんまり使い所がありません。 他に素敵な計算はないでしょうか。

指数関数(Exponentialボタン)

毎フレーム一定量を加算していく、という以外に、目的値に近づくための計算としては どんなものがあるでしょう。

いろいろありそうですが、足し算があるならかけ算もありそうです。 「毎フレーム目的値との差が0.9倍になっていく」というような計算はどうでしょう。

p += (p1 - p) * 0.1f;

p1が目的値、pが今の位置です。(p1-p)は目的値との差ですね。これに0.1を掛けたものをpに足すと、 目的値までの距離が90%になります。あと500kmだったものが450kmになるわけです。 そして次のフレームでもう一度計算すると、450kmの0.1倍である45km進みますから、 残り距離は405kmになります。こうしてどんどん近づいていくわけです。

実際に使う時には先程と同じく、Time.deltaTimeを用いて、 フレームレートに依存しないようにします。

p += (p1 - p) * 0.1f * Time.deltaTime;

deltaTimeを掛けるならば0.1のままでは遅すぎるので、 もっと大きくすることになるでしょう。

動き

では、この動きを見てみます。サンプルでExponentialを選んでください。

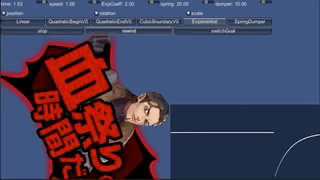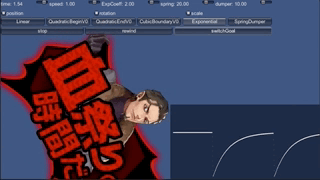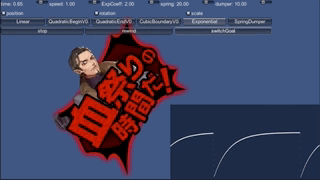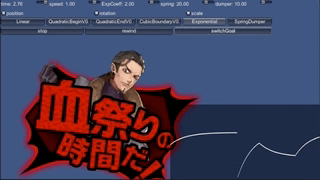
終わり速度0の二次関数に似ていますが、終わり方はもっと緩やかです。 また、逐次計算にしてあるので、途中でswitchGoalボタンを押して目的地を変えた場合、 そこから即座に反応してつなぎます。

ただ、終わりが緩やかすぎる気はします。 実はこの関数は、永遠に目的地に辿りつかないのです。 先程の計算を思い出してください。 例えば500kmから近づいていく例では、10回計算してもまだ174km残っています。 40回計算すればあと7.4kmまで近づきますが、ゼロにはなりません。 しばらく待てば止まるようには見えますが、それは 「遅すぎて止まってるように見えているだけ」で、 実はまだ動いているのです。

そして、それにかかる時間を簡単に指定することもできません。 画面上端中央あたりにExpCoeffとあり、その右にあるスライダーでいじれます。 これを先程の式の0.1の代わりに使います。 1だと、だいたい1秒後に63%(1-1/e。eは自然対数の底)くらいの所まで行きます。 2だと、だいたい1秒後に86%(1-1/e^2)くらいの所まで行きます。 「99%に到達するまでt秒かかるようなパラメータを計算する」というようなことはできますが、 90%がいいのか99%がいいのかは用途や趣味によりますので、結構面倒なところです。 私はとりあえず4を入れて様子を見ることが多いですが、根拠はありません。 二次関数や三次関数ならばt=1になれば最終値になるわけで、 これは結構面倒です。

理屈

さて、実はこれが指数関数になっているわけですが、それはどういうことでしょうか。 理屈に興味がない方は飛ばしていただいてかまいません。

指数関数補間

まず、普通に指数関数で補間することを考えましょう。

指数関数で2点を補間する場合、関数の形はp=a*exp(-k*t)+bという具合が便利です。 一次関数のtをexp(-k*t)で置き替えた感じです。 そして、expの中は負になるようにします。そうすれば、t=0でexpが1、tが無限大でexpが0になります。

p0 = a*1 + b
p1 = a*0 + b

から、b=p1、a=p0-p1と定まります。つまり関数形はp=(p0-p1)*exp(-k*t)+p1 です。kは好きに決めていい値です。動きの調整に使えます。

さて、先程書いた処理は、

p += (p1 - p) * 0.1f * Time.deltaTime;

というものでした。これを毎フレーム繰り返した結果が、p=(p0-p1)*exp(-k*t)+p1 という関数と同じ形をしているということです。

積分

何度も何度も何かを足して値を作っていく、というのは、つまるところ積分です。

先程の0.1づつ足していく話で考えましょう。0.1づつ足していってできる関数は、 一次関数p=at+bと同じでした。つまり、0.1を積分していくと一次関数になるということです。 逆に言えば、一次関数を微分すれば定数になるということで、その通りです。p'=aですね。 このaが0.1だったわけです。

つまり、ある関数を逐次計算に変えたければ、それを微分して毎フレーム足せばいいのです。 微分して積分すれば戻りますよね。

指数関数を微分してみる

では、指数関数を微分してみましょう。 まずexpの微分はexpですが、中のtに何か掛かってる場合は外に出して掛け算します。 exp(-k*t)は-k*exp(-k*t)になります。結果、

-k*(p0-p1)*exp(-k*t)

が微分です。あとは今の用途に合わせて変数の値を決めます。 常に「今から補間を開始する」ことにしてしまえば、 p0は今の位置pで置き替えられ、tはいつも0ということになります。 expの中身が0になるので、expは1になり、消えます。 ついでに先頭のマイナスを(p-p1)の中に入れて引き算をひっくり返し、 一番簡単なオイラー法での積分を行えば、

p += (p1 - p) * k * Time.deltaTime;

となります。オイラー法では、微分にTime.deltaTimeを掛けて今の値に足します。 kに0.1を入れれば、元の式と同じになります。

使用上の注意

このまま使う場合、たまに危険なことが起きます。 k * Time.deltaTimeが1より大きくなる場合を想像してください。 目的値より先に行ってしまいます。 さらに、2を超えると破滅的なことが起こります。

今「目的値まで100km」にいるとしましょう。今k * Time.deltaTimeが 3あったとすると、次のフレームの計算で「目的値を遥かに超えて逆側に突き抜け、距離が200kmに増える」 という恐ろしい状態になります。さらに次のフレームでは距離が400kmに増え、 どんどん遠ざかっていくのです。いずれはfloatの限界値を超えてinfinityに至り、 Unityの場合、これをTransformに入れたり頂点座標に入れたりすると、Unityごと落ちます(mac版のエディタだけ?)。 なので、この式を使う場合には、kの値には制限をかけておく必要がありますし、 Unityの設定 でMaximum Allowed Timestepをあまり大きすぎない値に設定しておくのも良いかと思います。 0.1くらいでいかがでしょうか。

それにしても、この問題ははどこから来たのでしょう。何か変な近似しましたっけ?

実は「オイラー法での積分を行えば」というところが問題です。 厳密に積分するのであれば、t=0からt=Time.deltaTime(長いので以下dt)までの定積分を求めて、 それを加算せねばなりません。幸い、今の場合はそれが簡単にできるので、 やってみましょう。積分した後の関数はわかっているので簡単です。 不定積分(p-p1)*exp(-k*t)に、t=dt を入れると(p-p1)*exp(-k*dt)になり、t=0を入れると(p-p1)になりますから、

(p - p1) * (exp(-k * dt) - 1)

が定積分になります。(p-p1)の向きを先程の式に合わせてコードにすると、

p += (p1 - p) * (1f - Mathf.Exp(-k * Time.deltaTime));

となります。いらない心配をしたくなければ、こちらの実装をしておく方が安心ではないでしょうか。

用途

指数補間は相当便利で、私は操作で横槍が入り得るものにはほとんど何でも使っています。 時刻の代わりに現在値を覚えておき、 単に目的値とパラメータ(上のcoefficient)を差し換えれば、勝手に補間されます。 どうせ現在値はRectTransformに入っていますので、 そこから値を取るのが面倒でなければ、現在値を取っておく必要もありません。 ボタン操作等々でバンバン目的値を差し換えても、それなりに補間されます。

ただし、パラメータをどれくらいにするかを決めるのが面倒なのと、 じわじわ動き続けて気持ち悪いのが難点です。 例えばパラメータが1だと、99%の位置に到達するまで4秒以上かかります。 にも関わらず、1秒足らずで50%の所を過ぎてしまうわけで、少々終わりが遅すぎです。 これが気に入らないのであれば、多少面倒でも二次関数を使う方が良いかもしれません。

なお、expで目的値に限りなく近づいていくような現象は自然界にはたくさんあります。 お湯が冷めていく時、その冷め方はexpです。 また、霧の日に対象物がどれくらい見えなくなるかの具合は、 距離を変数としたexpで決まります。 「変数が1増える度にN%に減る」的な現象はexpになります。 操作による横槍が入らない場合であっても、使える局面は多いかと思います。

バネダンパ(SpringDamperボタン)

もう一個面白い奴があるので紹介しましょう。 物理シミュレーションを応用するやり方です。

今、pにある物と、p1にある地面に刺さった杭を、バネで結ぶと想像してください。 このバネは元々すごく短くて、無理矢理伸ばして結んでいます。 手を離すと、pにあるものはp1に向かって引っぱられていきます。 そのうちバネの本来の長さに縮んで、そこで止まるでしょう。 pはだいたいp1の近くまで行くはずです。

これを使います。

物理シミュレーションと言っても難しくありません。 まず、加速度を計算する方法を用意します。 今の例ではバネが伸ばされていると、縮む方向に加速度をかけます。 あとは、毎フレーム加速度を積分、つまり加算して速度を計算します。 そして、その速度を積分、つまり加算して位置を計算します。

a = CalcAccel(); // 加速度を計算(aはaccelのa)
v += a * dt; // vはvelocityのv
p += v * dt; // pはpositionのp

毎度のことですが、dt(=Time.deltaTime)を掛けてから足すのは、フレームレートに 依存しないで同じような結果を得るためです。

あとは加速度の計算ですが、「目的値から遠いほど強くひっぱられる」 なので、こんな感じではいかがでしょうか。

a = (p1 - p) * spring; // p1は目的値

p1-pが大きいほどaは大きくなります。springは調整用の数で、 好きに設定できます。

とりあえず動きを見てみる

これで作った動きが、これです。

止まりません。

考えてみれば、現実世界でバネが止まるのは、摩擦があるからです。 摩擦がなければ、行き過ぎた上に同じ場所まで戻ってきて、永遠に振動します。 実は、加速度を先程の式で定めて積分した場合、 位置はsin関数になります。sinなので当然いつまでも振動するわけです。

というわけで、摩擦に相当するものを入れましょう。先に動きをご覧ください。

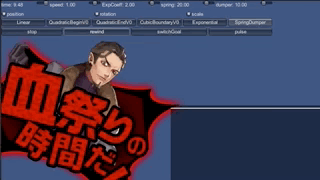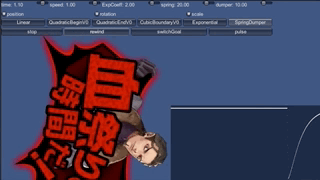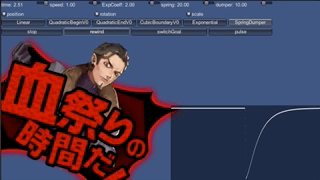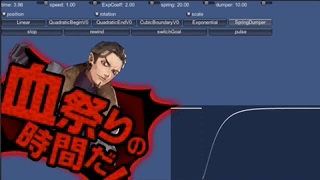
動きが落ちつきました。画面右上のdamperとあるスライダーを0でなくしたのが 先程との違いです。 「減衰させるもの」という意味のダンパーという言葉を使い、 この仕組みで制御することをmass-spring-damper systemと呼んだりします。

なお、damperの値を弱くすると、「ちょっと行き過ぎつつ戻って落ちつく」 という挙動にもできます。

現実世界のものは急停止できず、余裕をもって減速するか、行き過ぎて少し戻るかになりますが、 それと同じです。damperを強くすれば余裕をもって減速し、弱くすれば行きすぎてから戻るわけです。

コード

計算関数は以下のようになっています (サンプル内の相当するコード)。

float a = ((p1 - p) * spring) - (v * damper);
v += a * dt;
p += v * dt;

aが加速度で、目的値と現在値の差にspringを乗じて足して加速し、 速度にdamperを掛けた分を引くことで減速させます。

特徴

このバネダンパ方式は、指数関数よりも始めが滑らかになる点が特徴的です。 指数関数は目的値を切り換えた瞬間が最大速度ですが、 こちらの場合は加速に多少時間がかかります。 そして、振動させられるのも他にない特徴です。

正直に言えば、指数関数ほど使い勝手は良くありません。 パラメータが二つあって調整が面倒ですし、 指数補間以上に落ちつくのにどれくらいかかるのか読めません。 指数補間なら「1秒後に63%」のようなことが言えましたが、 こちらは「パラメータをいくつにすればどうなるのか」がわかりにくいのです。

しかし、振動が欲しい時には合いますし、 反応が鈍い方がいい用途もあります。 さらに、毎フレーム目標値を変える場合には、落ちつくまでの時間が 計算しにくいことはあまり問題ではありません。 こういった特徴は例えばカメラ制御には合います。 ゲーム中の操作に追随して目的値を次から次へと変える必要があり、 反応は鈍い方がリアルで、かつ、少し行き過ぎて戻る振動がまたリアルさを感じさせます。

もう一つ、この方式は途中で突発的な動きを混ぜるのが楽です。 例えば、キャラAを追いかけるキャラBに対して、 誰かがボールをぶつけてはじき飛ばした、というようなケースです。 サンプルプログラムでSpringDamperを選んでいると、 下段にpulseというボタンが現れます。これを押すと、 速度に直接値を加えることで跳ね飛ばします。

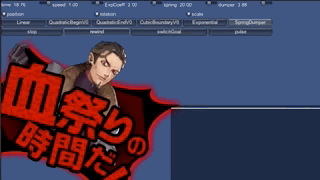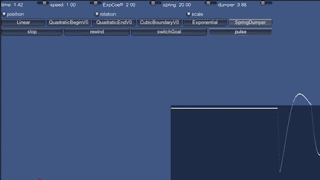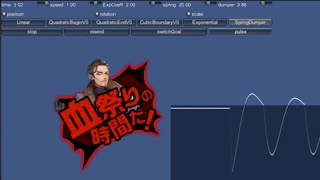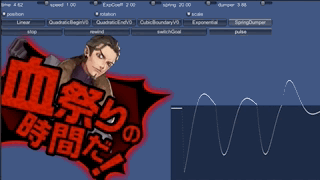
いつどのように邪魔されても、それなりにそれっぽい動きをしながら目的値に向かいます。 これは速度を持っているからこそできることです。

使用上の注意

指数関数の時に、「オイラー法で積分したら宇宙の果てに飛んでいってUnityが死んだ」 というお話をしました。 今回も同じことが起きます。 もう一度コードをご覧ください。

float a = ((p1 - p) * spring) - (v * damper);
v += a * dt;
p += v * dt;

springやdamper、そしてdtが大きくなると、宇宙の果てに飛ぶことになります。

damperの調整範囲

まずはdamperから考えます。springを0としてみましょう。すると、

v += -v * damper * dt;
p += v * dt;

となります。damper * dtが1より大きいと、速度が反転していまいます。 指数関数の時に目標値を追い抜いたのと同じですね。2を超えると、 速度がどんどん大きくなって、いずれUnityを殺します。

というわけで、damperには制限をかける必要があります。 damper * dtが1を超えないように、調整範囲を制限しましょう。 つまり、

maxDamper = (1f / Time.maximumDeltaTime);

ということです。

springの調整範囲

次にspringの調整範囲を考えます。damperを0としてましょう。

v += (p1 - p) * spring * dt;
p += v * dt;

このままだとよくわからないので、「つまり位置はどうなるわけ?」というのを考えるために、 下の行のvを、上の行の計算で置き替えます。

p += (v * dt) + ((p1 - p) * spring * dt * dt);

vがどうなっているかはわかりませんが、とりあえずspring * dt * dt が1を超えると、pがp1を追い越しそうです。 spring * dt * dt < 1ということは、つまり、

var maxDt = Time.maximumDeltaTime;
maxSpring = (1f / (maxDt * maxDt));

としておくのが無難だろう、ということになります。 最大でTime.deltaTimeが0.1になるのであれば、 springの最大値は100です。それ以上をつっこむと、 行きすぎたり、宇宙の果てに飛んだりする恐れがあります。

なお、指数関数の時のように、オイラー法で近似せずに、きちんと定積分を計算することも可能だと思います。 Wikipediaや、 この文書 が助けになるでしょう。でも相当面倒くさいので私はやっていません。

なお以下は、これを使って試しに作ってみたボタン とポップアップ です。バネダンパなので、若干行きすぎて戻る挙動が表現でき、途中で違う動きにつなぐことも容易です。ただし調整には慣れがいります。

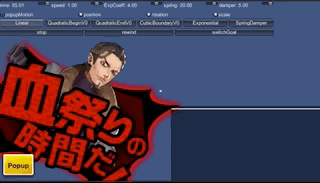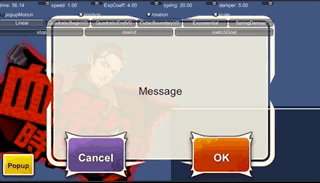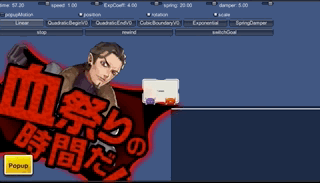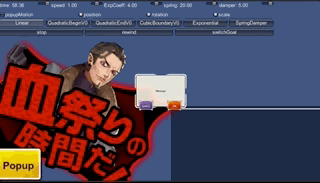
関数は他にもある

さていろいろ見てきましたが、補間に使える関数は他にもたくさんあります。パッと浮かぶだけでも、

• 4次以上の多項式
• 三角関数
• 逆数
• 平方根、立方根
• 対数

というくらいはありますね。条件が満たされればこれらを使って補間をするのも 良いと思います。 ただ、私自身はあまり用途が思い浮かびません。 単純に振動させたい時に三角関数を使うことがある、という程度ですが、 バネダンパでいい気もします。途中で何かぶつけて乱したりもできますし。

終わりに

数学の臭いが少し強くなりましたが、「動き」=「数値の変化」=「関数」 ですから、どうしてもそうなってしまうのです(数学は苦手なので書くのは苦労しました)。

しかしこの話は、

• カメラ制御
• 3D回転の補間(クォータニオンの利用)
• AIで動くキャラクターの動き制御

といった話題につながる基礎で、奥深く、しかもゲームの遊び勝手に結構関わってくる分野です。 私もこれから修行を積んで、そういった分野で成果が出せるように がんばろうと思っております。