LobiでAndroidをやってますうえだです。
Tech KAYAC Advent Calendar 2016の10日目の記事を書かせていただきます。
よろしくお願いします！
業務で携わった「Androidでアプリを録画した話」について書こうか、
完全業務外の「ナンバーリンクというやつをいい感じに解こうとした話」について書こうか迷いましたが、
(個人的に)ロマンが溢れてる後者について書くことにしました。
あらすじ
最近、ナンバーリンクというペンシルパズルのアプリを作っています。
ナンバーリンクとは以下のようなパズルです。
こんな風に盤面に数字が配置されていて、
こんな風にいい感じに同じ数字を繋げればクリアです。
ルールはこんな感じです。
- 線は隣接したマスを縦横に通っていく。
- 1マスを2本以上の線が通ってはいけない。交差したり別れたりしてはいけない。
（「すべてのマスを線が通ってなければいけない」というルールがあることもあります。）
さて、このような問題をただひたすら解き続けるアプリを作っているのですが、その中で一番辛かったのが問題の量産でした。
小さい問題から大きい問題まで200題ほどを、コツコツコツコツ作っていたのですが、それがまったく楽しくない作業だったのです。
そして今後、「デイリーで問題配信したい」などと構想し始め 、ちまちま問題を手作りなどしていられなくなりました。
なので、問題を自動で量産する仕組みを作ろうと考え始めました。
しかしこれは相当厄介で、
ナンバーリンクは巷では「かなり問題を作りづらいし、解きづらいペンシルパズル」と言われていたりします。
実際、それっぽい問題を自動生成するアルゴリズムを考えてはみたものの、単純でしょうもないカスのような問題しか産みだしてくれませんでした。
そこから、いろいろ試行錯誤したりぐぐったりした結果、いい感じの問題が作れそうな手順を導き出しました。
これです。
- 盤面にランダムに数字を配置！
- それがいい感じの問題か判定！
- いい感じの問題でなかったら、1からやり直す。
とても馬鹿っぽいですが、
- ランダム性によってくせのない問題になる（かもしれない）
- デイリーで問題配信となると、短時間で膨大な数を作る必要はないため、多少時間がかかってもいい
と考えた故です。
（1.については、もちろん完全ランダムに数字を配置するのではなく、少しいろいろ工夫していますが、 そこらへんの話は省略しています。）
ここで重要なのは、2の「いい感じの問題か判定する」方法です。
ここももちろん、人力でなく、自動かつ高速でやらなければ話になりません。
長くなってしまいましたが、この「いい感じの問題の判定方法」についてが 「ナンバーリンクをプログラマチックに解こうとする話」になります。
この課題に、組合せ最適化問題の考え方を用いてアプローチしました。
組合せ最適化問題について
かなりざっくりにいうと、組合せ最適化問題とは、(非連続な)いくつか状態の組合せから、条件を満たし、かつ最適なものを見つける問題です。
ナンバーリンクは組合せ最適化問題といえます。
例えば次の問題
を組合せ最適化問題の要素である、「状態」、「条件」、「最適化するもの」に当てはめると、以下のようになります。
状態:
各マスが取りうる状態です。
ナンバーリンクは「空白マス」と「数字マス」があり、
空白マスは以下のいずれかの状態をとります。
また数字1のマス、2のマスは以下のいずれかの状態をとります。
これら状態を組合せは、
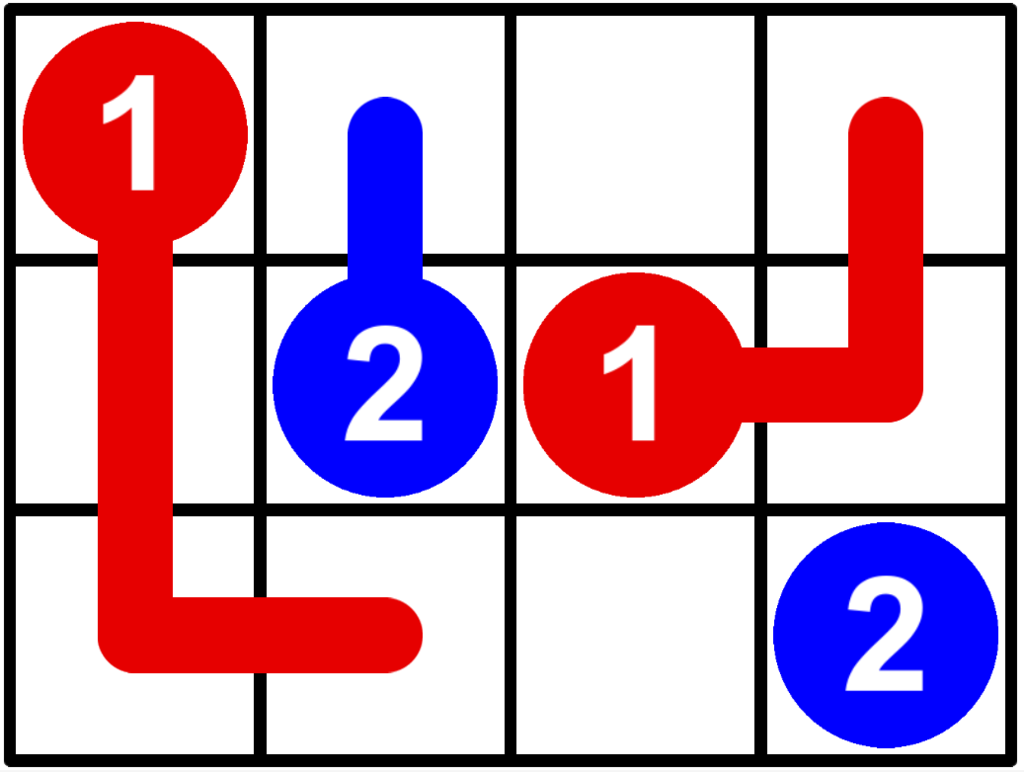
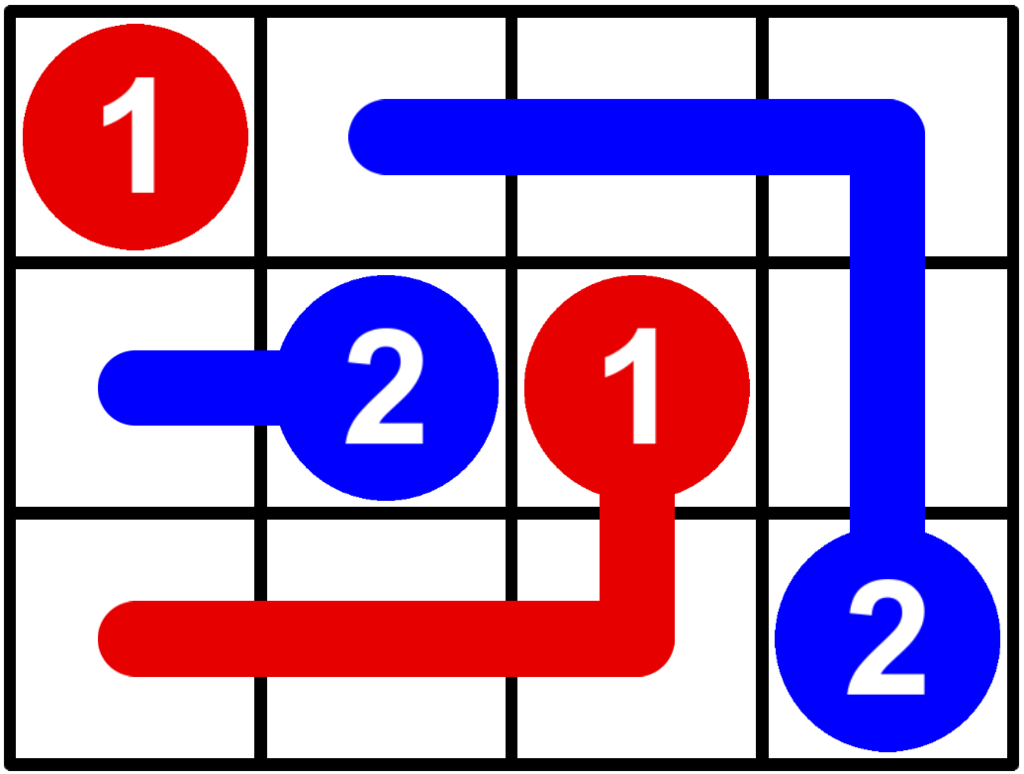
といったものになったりします。
条件:
状態の組合せが、ナンバーリンクの解として成立していること。 上図で言えば下の2つです。
最適化するもの:
空白マスの数をなるべく少なくする（空白マスの数が0である解を探すため）。
このような要件のとき、条件を満たしてかつ状最適解と呼べる状態の組合せは、
だけになります。
なぜ組合せ最適化問題として扱うか
なぜナンバーリンクを組合せ問題として扱うか。
それは、プログラムで解きやすいためです。
組合せ最適化問題の実態は、整数だけの最適化問題です。 つまり、
のような問題です。
条件を満たし、かつを最大化するような
、
、
を求めよ、というやつです。
ナンバーリンクの実態はこういうやつです。 そしてその最適化問題を解けば、ナンバーリンクの解が得られます。
数式が出てきて嫌な感じになる人もいると思いますが、 こういう問題を解くソフトウェアは、フリーのものから商用のものまでたくさんあるので無問題です(GLPK、SCIP、CPLEXなど)。
ここで重要なのは、ナンバーリンクの定式化の方法さえ知っていれば、 ナンバーリンクの解き方は知らなくても問題は解けるということです。 そしてこの考え方は、世の中の組合せ最適化問題の構造を持つあらゆる問題に通じています。
世の中には組合せ最適化問題といえるものがたくさんあります。 同じペンシルパズルである魔法陣、ピクロス、数独や、将棋、囲碁、オセロのようなゲーム、 さらには経路探索、電車の乗り継ぎ、仕事のスケジューリング、翻訳などなど。
ただしそれらの問題すべてそういうフローで解決できるかというと、実際はまったくそんなことはありません。 以下の壁に突き当ることが多いためです。
- 問題の正確な定式化が難しい。
- 問題が大きくなると、だいたい計算量がえらい勢いで増える。
実はナンバーリンクも例外でなく、2.の問題を抱えています。
ナンバーリンクを組合わせ最適化問題として扱うことの落とし穴
ナンバーリンクは、問題の盤面の大きさや配置する数字の数が増加すると、
組合せ数がえらい勢い増えて(いわゆる組合せ爆発して)しまい、
必要な計算量もえらい勢いで増えて(いわゆる指数関数的に増加して)しまいます。
なので、なるべく状態数が少なくなるように定式化する、といった工夫をしなければ、
現代のコンピュータでも、15×15の盤面の問題を解くのにさえ100年以上かかったりしてしまいます。
ちなみに、ナンバーリンクを効率的に解く方法を人類はまだ見つけていません。
もしナンバーリンクを効率的に解く方法を見つけることができたら、数学史に名を残せます！
（詳しくは、「ナンバーリンク NP完全性」でググってみてください。だいぶロマンが溢れています。）
結局、ナンバーリンクの問題生成は自動化はできるのか。
これからやってみるのでまだ分かりません（すみません......）が、 そこまで盤面が大きくなければ、できそうな気はします。
- 盤面にランダムに数字を配置。
- それがいい感じの問題か判定する。
- いい感じの問題でなかったら、1からやり直す。
の「2. いい感じの問題か判定する」に組合せ最適化問題の考え方を用いますが、ここがよさげに高速できるかどうかにかかっています。
おそらくいろいろ工夫すれば、10×10くらいまでの問題なら、なんとか自動生成できるのではと考えています。
ナンバーリンクをプログラマチックに解こうとする
上の方で示した組合せ最適問題への定式化は、だいぶ概念的でした。
もう少ししっかりプログラム的に解けるよう定式化し、「いい感じの問題か判定する」をどのようにしようとしているか、
最後にそれを示して終わりたいと思います。
いい感じの問題について
のように、空白マスを残したままの解を、ナンバーリンク用語で短絡解といいます。 このような短絡解が存在する問題は、ナンバーリンク界では「いい感じでない問題」とされることがあるため、それに倣います。
なので、「それがいい感じの問題か判定する」は、「解が存在し、かつ短絡解が存在しない問題か判定する」とします。
- 盤面にランダムに数字を配置する。
- 1の問題に、解が存在し、かつ短絡解が存在しないか判定する。
- そんな問題でなかったら、問題を作り直す。
（もちろん2を満たすからといって優れた問題になっているとは限りませんが、 ここではこれ以上細かいことには触れないことにします。）
定式化
先ほどと同じように、「状態」、「条件」、「最適化するもの」を考えてます。
先ほどはだいぶざっくりしていましたが、もう少し数学的な変数を使ったりしてみます。
また、短絡解が存在しない問題であるか判定するを考慮するようにします。
以下のナンバーリンクの問題を例として考えてみます。
数字は1、2、マスはから
までです。
数字の集合、マスの集合を
、
とします。
また、あるマスの隣にあるマスの集合を
とします
（例えば ）。
状態:
以下の変数で表します。
マスに数字
の線(数字
マスへ数字
例えば
の状態のとき、
は数字1の線が通るため、
、
は数字1の線でつながっているため、
、
は数字1の線でつながっているため、
、
になります。
なぜどの状態も0 or 1で表しているかというと、次の条件を考えるとき、その方がやりやすいためです。
条件:
ここではざっくり考えます（計算量を減らすには、しっかり考える必要があります）。
条件1 あるマスにはある数字の線が通る、または空白のまま。
「をある数字の線が通る」は、「
には、1か2の線いずれか1本通る」なので、
。
または空白のままは、
。
とできます。
この条件式は
とまとめられます。
条件2 あるマスが数字マスでないとき、
- 数字
のいずれか2マスと
とすると、
「は
いずれか2つマスと
の線でつながっている」は
、
逆に「の線でつながってない」は、
という式で表せます。
これも次の1つの式にまとめられます。
さらにもう少し一般的に書くと、
となります。
条件3 あるマスが数字
のマスのとき、
の線でつながっている。
- 逆にそれ以外の数字の線ではつながっていない。
これは条件2とほぼ同じ感じで、
で表せます。
また、は
のマスなので、
です。
最適化するもの:
「空白のマスをなるべく多くする」= 「線の入るマスを少なくする」、つまり
が最小になるようにする。
以上の状態、条件、最適化するものをまとめてもう少しそれっぽく書くと、
以下のようになります（と思います。あまり数式に自信がない）。
ただしは数字1のマスの集合(
)、
は数字2のマスの集合(
)、
はそれ以外のマスの集合、を表しています。
minimizeは最適化する式、subject toは条件式、を表しています。
問題を解くと
この最適化問題を、最適化問題ソフトで解いたりすると、
...
のような結果が得られます。
するとには1の線が通過する、などということがわかるので、その情報を組み立てると
という解が得られます！
またこの解は、最適化の条件より、問題の中で「最も線の通過するマスが少ない」（=空白マスが多い）パターンです。
つまりこの解が短絡解でないということは、この問題には短絡解がなく、したがって「これはいい問題である」ことが確認できます。
は線の通過するマスの数を示しているので、「
= マスの数」かどうかで、「短絡解があるか」どうかがわかります。
また、もしそもそもこの問題がナンバーリンクとして解けない場合、最適化問題ソフトはしっかり解がないことを教えてくれます。
ちなみに
この方法による定式化では、
4×4の盤面で数字が1〜3ぐらいであれば、状態を表す変数は76、条件式の数は46はになりましたが、
10×10の盤面で数字が1〜8までとかになると、状態の変数は1906、条件式の数は838はまで膨れ上がりました
（数字マスが端にあるかなどで、数は多少増減します）。
まとめ
- ナンバーリンクは、組合せ最適化問題的に考えると、それほど大きくない盤面の問題なら、自動的かつそれなりの時間で解けそう。でも工夫は必要そう。
- 問題を作る人を雇った方が効率が良さそう。
終わりに
- はてなぶろぐは数式扱うのが辛い
- 定式化の話は、間違っている気もするので、おかしなところがあればご指摘いただけると大変ありがたいです。
- 明日は @pocke-pocke-pocke さんによる(おそらく)トレンディーな話です！
- カヤックUnityアドベントカレンダー も熱いです！
